Преобразование как изменение систем координат

Мы рассматриваем преобразование множества точек, принадлежащих объекту, в некоторое другое множество точек, причем оба этих множества описаны в одной и той же системе координат. Таким образом, система координат остается неизменной, а сам объект преобразуется относительно начала координат до получения желаемого размера. Другим эквивалентным способом описания преобразования является смена систем координат. Такой подход оказывается полезным, когда желательно собрать вместе много объектов, каждый из которых описан в своей собственной локальной системе координат, и выразить их координаты в одной глобальной системе координат. Существует и еще один, третий подход, при котром происходит изменение глобальной системы координат по отношению к локальной системе координат объекта (см. рис.2.7).

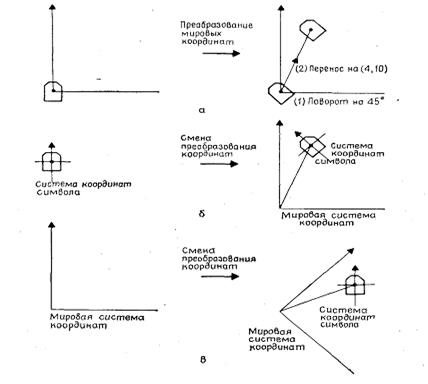
Рис. 2.7. Преобразования как изменение системы координат

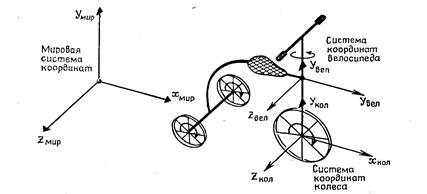
Рис. 2.8. Пример преобразования с изменением системы координат

Описание всех объектов (символов) в мировой системе координат и последующее размещение их в желаемом месте, приводит до некоторой степени к нереалистичному изображению всех символов, первоначально заданных один поверх другого в одной и той же мировой системе координат. Более естественно полагать, что каждый символ задан в своей собственной системе координат и затем промасштабирован, повернут и перенесен путем преобразования координат в новую мировую систему координат. Второй подход легко представить себе как сжатие или растяжение, поворот и позиционирование на мировой координатной плоскости отдельных листков бумаги, на каждом из которых изображен символ (или наоборот, сжатие или растяжение, поворот и перемещение плоскости относительно каждого из листков бумаги). С математической точки зрения оба подхода идентичны.

Подход, основанный на изменении систем координат, удобен в тех случаях, когда задается дополнительная информация для подобъектов в их локальных системах координат. Например, если к переднему колесу трехколесного велосипеда (рис. 2.8) приложить крутящий момент, то все его колеса повернутся. Нам необходимо определить, насколько велосипед переместится в пространстве как единое целое. Эта задача более сложная, чем та, которая связана с размещением символов, поскольку здесь требуется несколько последовательных изменений систем координат. В начальный момент системы координат велосипеда и его переднего колеса заданы относительно мировой системы координат. При движении велосипеда вперед переднее колесо поворачивается вокруг оси z системы координат колеса, и одновременно системы координат колеса и велосипеда перемещаются относительно мировой системы координат. Системы координат колеса и велосипеда связаны с мировой системой координат с помощью зависящих от времени переносов вдоль осей x и у иповорота вокруг оси у. Координатные системы велосипеда и колеса между собой связаны с помощью зависящего от времени поворота вокруг оси у, вызываемого поворотом руля. (Система координат велосипеда связана с рамой велосипеда, а не с рулем).