Преобразование координат
Сначала рассмотрим общие вопросы преобразования координат. Пусть задана п-мерная система координат в базисе (k1, k2,.... kn), которая описывает положение точки в пространстве с помощью числовых значений кi. В КГ наиболее часто используются двумерная (n = 2) и трехмерная (n = 3) системы координат.
Если задать другую, N-мерную, систему координат в базисе (m1, m2,..., т) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:
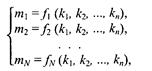
где fi — функция пересчета i-й координаты, аргументами являются координаты в системе ki,. Можно поставить и обратную задачу: по известным координатам (m1, m2,.... т) определить координаты (к1, k2,..., кn ). Решение обратной задачи запишем так:
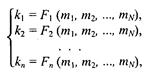
где Fi — функции обратного преобразования.
В случае если размерности систем координат не совпадают (п ≠ N), осуществить однозначное преобразование координат чаще всего не удается. Например, по двумерным экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов.
Линейные преобразования наглядно записываются в матричной форме:
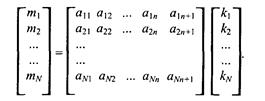
Здесь матрица коэффициентов (аij) умножается на матрицу-столбец (ki), и в результате будем иметь матрицу-столбец (mi ).
Мы и дальше часто будем использовать умножение матриц, поэтому сделаем небольшой экскурс в матричную алгебру. Для двух матриц —
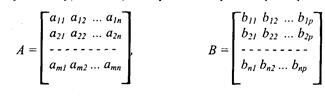
матрицы А размерами (т х п) и В — (n x p):
матричным произведением является матрица С = АВ размерами (m х р):
С =  для которой элементы cij рассчитываются по формуле
для которой элементы cij рассчитываются по формуле 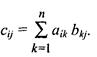
Дата добавления: 2015-01-29; просмотров: 991;
