Простейшие двумерные преобразования

Точки на xy-плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точки Р(х, у), которая перемещается в новую точку Р'(х, у), сдвигаясь на Dx единиц параллельно оси x и на Dy единиц параллельно оси у, можно написать уравнения:

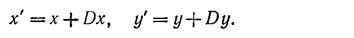
На рис. 2.1 показана точка с координатами (1, 2), которая смещается на расстояние (5, 7), преобразуясь в точку (6, 9). Определяя векторы-строки

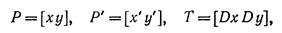
можно переписать это уравнение в векторной форме или более кратко

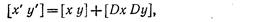
Объект можно перенести, применяя вышевыведенное уравнения к каждой его точке. Однако, поскольку каждый отрезок, описывающий объект, состоит из бесконечного числа точек, такой процесс длился бы бесконечно долго. К счастью, все точки, принадлежащие отрезку, можно перенести путем перемещения одних лишь крайних точек отрезка и последующего вычерчивания нового отрезка между получившимися в результате точками. Это справедливо также для масштабирования (растяжения) и поворота. На рис. 2.1 показан результат действия на контур домика операции переноса на расстояние (3, -4).

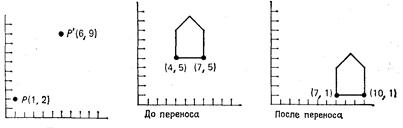
Рис. 2.1 Простейший перенос

Точки можно промасштабировать (растянуть) в Sx раз вдоль оси x: и в Sy раз вдоль оси у, получив в результате новые точки, с помощью умножения

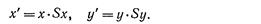
Определяя S как 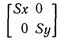, можно записать в матричной форме

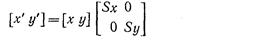
или

На рис. 2.2 отдельная точка (6, 6) масштабируется с коэффициентами 1/2 по оси X и 1/3 по оси у. На этом же рисунке показан контур домика, промасштабированный с коэффициентами 1/2 по оси x и 1/4 по оси у. Отметим, что масштабирование производится относительно начала координат; в результате преобразования домик стал меньше и ближе к началу координат. Если бы масштабные множители были больше 1, то домик увеличился бы и отдалился от начала координат. Способы проведения масштабирования относительно других точек, отличных от начала координат, рассматриваются в одном из последующих разделов главы. Пропорции домика также изменились· было применено неоднородное масштабирование, при котором Sх≠ Sу. Однородное масштабирование, для которого Sx=Sy, не влияет на пропорции.

Точки могут быть повернуты на угол θ относительно начала координат, как показано на рис. 2.2 для точки Ρ (6, 1) и угла θ = 30°. Математически поворот определяется следующим образом:

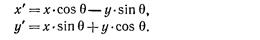
В матричной форме мы имеем

или

где через R обозначена матрица поворота. На рис. 2.2 показан квадрат, повернутый на 45°. Как и в случае масштабирования, поворот производится относительно начала координат.

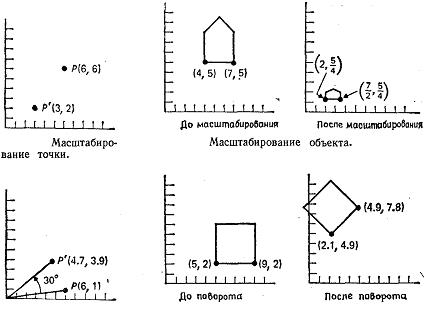
Рис. 2.2 Простейшие поворот и масштабирование