Последовательное соединение потребителей переменного тока. Треугольник напряжений и сопротивлений.
В схеме, состоящей из последовательно соединенных активного сопротивления, индуктивности и емкости (рис. 2.23), заданы приложенное напряжение U, частота f и числовые значения параметров R, L и С. Требуется найти ток и напряжения на элементах
| В последовательной цепи общим для всех элементов является протекающий по ним ток, поэтому именно с него начинаем построение векторной диаграммы. Проводим его изображение горизонтально (рис. 2.24). | 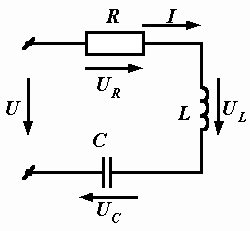 Рис. 2.23. Последовательная цепь переменного тока Рис. 2.23. Последовательная цепь переменного тока
|
Вообще, направление первого вектора при построении диаграмм произвольно. Оно диктуется соображениями удобства. Дальше мы должны показать векторы напряжений на всех элементах и в соответствии со вторым законом Кирхгофа в векторной форме 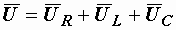 получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
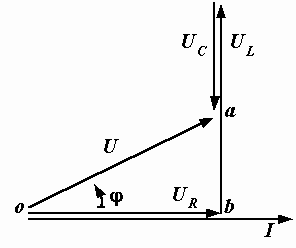
Рис. 2.24. Векторная диаграмма последовательной цепи
Нам известно, что напряжение на активном сопротивлении совпадает по фазе с током, поэтому вектор UR мы направляем по вектору I. К его концу пристраиваем вектор UL и направляем его вверх, так как напряжение на индуктивности опережает ток на 90° . Напряжение UС находится в противофазе с UL, т.е. отстает от тока на тот же угол 90° , поэтому вектор UС, пристроенный к концу вектора UL, направлен вниз. Векторная сумма UR, UL и UСдает вектор приложеного напряжения U.
Величины напряжений на отдельных элементах цепи нам известны:
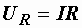 ,
, 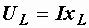 ,
, 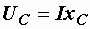 . (2.23)
. (2.23)
Из треугольника 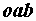 (рис. 2.24) по теореме Пифагора находим
(рис. 2.24) по теореме Пифагора находим
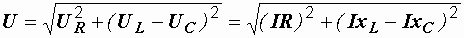 .
.
Вынося 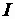 из под знака радикала, записываем последнее выражение в виде:
из под знака радикала, записываем последнее выражение в виде:
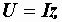 , (2.24)
, (2.24)
где z – полное сопротивление цепи, равное
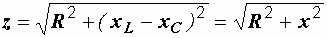 . (2.25)
. (2.25)
В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = хL – xC. Сами индуктивность и емкость называются реактивными элементами, и их сопротивления хL и xCтоже носят названия реактивных.
Выражение (2.24) называется законом Ома для всей цепи. Оно может быть записано и так:
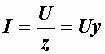 , (2.26)
, (2.26)
где 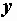 – полная проводимость цепи, представляющая величину, обратную полному сопротивлению:
– полная проводимость цепи, представляющая величину, обратную полному сопротивлению: 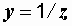 .
.
Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений 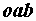 (рис. 2.24):
(рис. 2.24):
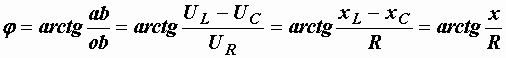 .
.
Векторная диаграмма на рис. 2.24 построена для случая, когда 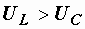 , что имеет место при
, что имеет место при 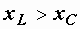 , когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.
, когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.
Возможны также режимы, когда 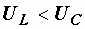 и
и 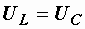 . Вернемся к векторной диаграмме, представленной на рис. 2.24. Изобразим отдельно треугольник oab, являющийся ее частью (рис..
. Вернемся к векторной диаграмме, представленной на рис. 2.24. Изобразим отдельно треугольник oab, являющийся ее частью (рис..
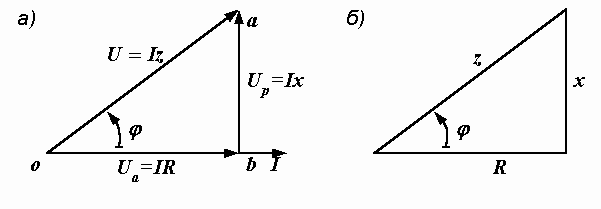
Рис. 2.28. Треугольники напряжений (а) и сопротивлений (б)
Проекция вектора напряжения на вектор тока называется активной составляющей напряжения. Она обозначается Uа и равна падению напряжения на активном сопротивлении 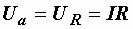 . Реактивная составляющая напряжения Uр – это проекция вектора напряжения на направление, перпендикулярное вектору тока. Она равна падению напряжения на суммарном реактивном сопротивлении цепи
. Реактивная составляющая напряжения Uр – это проекция вектора напряжения на направление, перпендикулярное вектору тока. Она равна падению напряжения на суммарном реактивном сопротивлении цепи 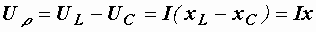 . Как видно из рис. 2.28, если все стороны треугольника напряжений разделить на ток, то получится подобный ему треугольник сопротивлений (рис. 2.28,б). Ему соответствуют следующие формулы:
. Как видно из рис. 2.28, если все стороны треугольника напряжений разделить на ток, то получится подобный ему треугольник сопротивлений (рис. 2.28,б). Ему соответствуют следующие формулы:
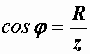 ,
, 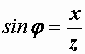 ,
, 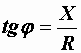 ,
, 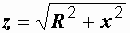 .
.
13. Параллельное соединение потребителей переменного тока. Треугольник проводимостей. 





Дата добавления: 2015-01-29; просмотров: 2163;
