Последовательное соединение индуктивно связанных элементов
Пусть две катушки, обладающие сопротивлениями 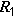 и
и 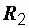 , индуктивностями
, индуктивностями 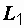 и
и 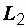 и взаимной индуктивностью
и взаимной индуктивностью 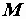 , соединены последовательно (рис. 3.3).
, соединены последовательно (рис. 3.3).

Рис. 3.3. Последовательное соединение индуктивно связанных элементов
Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой (рис. 3.3, а). Токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу. При встречном включении катушек конец второй присоединяется к концу первой (рис. 3.3, б).
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:
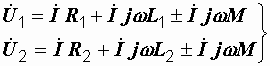 (3.1)
(3.1)
Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений
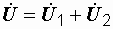 . (3.2)
. (3.2)
Входное комплексное сопротивление цепи получим из совместного рассмотрения трех последних уравнений
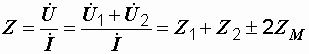 , (3.3)
, (3.3)
где 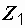 и
и 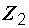 – комплексные сопротивления катушек, а
– комплексные сопротивления катушек, а 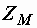 – комплексное сопротивление взаимной индукции:
– комплексное сопротивление взаимной индукции:
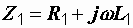 ,
, 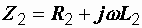 ,
,  .
.
Из (3.3) вытекают формулы, определяющие общую индуктивность цепи и суммарное индуктивное сопротивление:
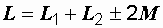 ,
, 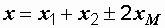 ,
,
причем 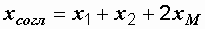 ,
, 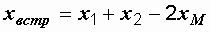 ,
,
т.е. 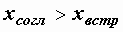 .
.
Можно определить результирующее индуктивное сопротивление каждой катушки. У первой оно равно 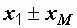 . И здесь при согласном включении оно больше чем при встречном. Физически это объясняется тем, что в первом случае магнитный поток, охватывающий каждую катушку, больше чем во втором; например, для первой катушки
. И здесь при согласном включении оно больше чем при встречном. Физически это объясняется тем, что в первом случае магнитный поток, охватывающий каждую катушку, больше чем во втором; например, для первой катушки 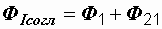 , а
, а  . Вследствие этого ЭДС электромагнитной индукции, оказывающая току индуктивное сопротивление, при согласном включении больше, чем при встречном.
. Вследствие этого ЭДС электромагнитной индукции, оказывающая току индуктивное сопротивление, при согласном включении больше, чем при встречном.
На рис. 3.4 изображены векторные диаграммы, построенные по уравнениям (3.1) и (3.2).
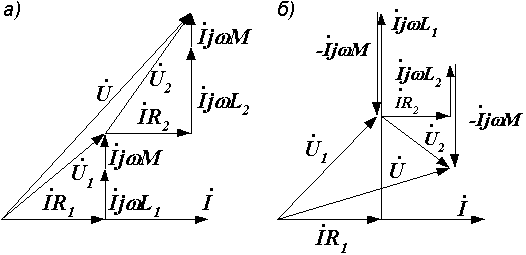
Рис. 3.4. Векторные диаграммы последовательной
цепи при согласном (а) и встречном (б) включениях
При встречном включении возможен так называемый "емкостный" эффект, когда у одной из катушек напряжение на зажимах отстает по фазе от тока (напряжение 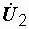 на рис. 3.4, б). Это имеет место, когда индуктивность катушки меньше величины взаимной индуктивности. В этом случае результирующая индуктивность рассматриваемой катушки (с учетом взаимной индукции) отрицательна:
на рис. 3.4, б). Это имеет место, когда индуктивность катушки меньше величины взаимной индуктивности. В этом случае результирующая индуктивность рассматриваемой катушки (с учетом взаимной индукции) отрицательна: 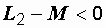 . Для всей цепи такой эффект невозможен. Ее индуктивность всегда положительна, и цепь носит активно-индуктивный характер.
. Для всей цепи такой эффект невозможен. Ее индуктивность всегда положительна, и цепь носит активно-индуктивный характер.
Пример 3.2. В схемах рис. 3.3 производились измерения напряжения, тока и активной мощности на входе цепи. При согласном (с) и встречном (в) включениях приборы дали следующие показания:  220 В,
220 В, 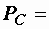 150 Вт,
150 Вт, 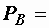 234,5 Вт,
234,5 Вт,  1 А,
1 А, 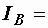 1,25 А. Чему равна взаимная индуктивность катушек, если частота питающего напряжения
1,25 А. Чему равна взаимная индуктивность катушек, если частота питающего напряжения 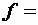 50 Гц?
50 Гц?
Р е ш е н и е. Определим полные, активные и реактивные сопротивления обеих схем
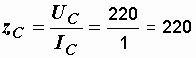 Ом,
Ом, 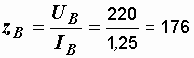 Ом,
Ом,
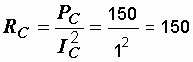 Ом,
Ом, 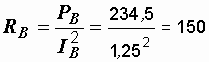 Ом.
Ом.
При переключении катушек с согласного соединения на встречное общее активное сопротивление цепи не меняется. Оно остается равным сумме их активных сопротивлений.
 161 Ом,
161 Ом, 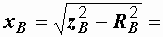 92,1 Ом.
92,1 Ом.
Так как 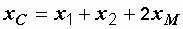 , а
, а 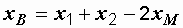 , то сопротивление взаимной индукции
, то сопротивление взаимной индукции
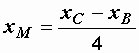 , а
, а 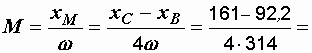
= 0,0548 Гн = 54,8 мГн.
Пример 3.3. Катушки, включенные по схеме рис. 3.3, б, имеют следующие параметры 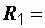 18,5 Ом,
18,5 Ом, 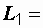 40 мГн,
40 мГн, 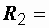 10,3 Ом,
10,3 Ом,  90 мГн,
90 мГн, 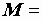 48 мГн. Частота источника
48 мГн. Частота источника 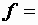 50 Гц, его напряжение
50 Гц, его напряжение  220 В. Определить показания вольтметра, подключенного к зажимам второй катушки.
220 В. Определить показания вольтметра, подключенного к зажимам второй катушки.
Р е ш е н и е. Определим сопротивления элементов и полное сопротивление цепи
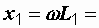 314 x 0,04 = 12,6 Ом,
314 x 0,04 = 12,6 Ом, 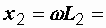 314 x 0,09 = 28,3 Ом,
314 x 0,09 = 28,3 Ом,
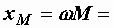 314 x 0,048 = 15,1 Ом,
314 x 0,048 = 15,1 Ом, 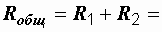 28,8 Ом,
28,8 Ом,
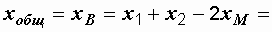 10,7 Ом,
10,7 Ом,
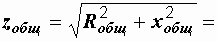 30,7 Ом.
30,7 Ом.
Ток, протекающий по цепи: 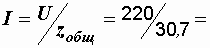 7,17 А. Сопротивление второй катушки с учетом взаимной индукции
7,17 А. Сопротивление второй катушки с учетом взаимной индукции 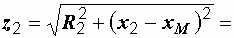 16,7 Ом; напряжение на ее зажимах
16,7 Ом; напряжение на ее зажимах 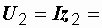 119,7 В.
119,7 В.
Пример 3.4.Последовательно с двумя соединенными согласно катушками, индуктивности которых  90 мГн и
90 мГн и 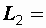 40 мГн, включен конденсатор емкостью
40 мГн, включен конденсатор емкостью 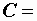 65 мкф. Частота источника
65 мкф. Частота источника 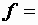 50 Гц. Взаимную индуктивность катушек можно менять, меняя их взаимное расположение (такие устройства, состоящие из двух взаимно перемещающихся катушек, называются вариометрами). При какой магнитной связи в цепи наступит резонанс напряжений?
50 Гц. Взаимную индуктивность катушек можно менять, меняя их взаимное расположение (такие устройства, состоящие из двух взаимно перемещающихся катушек, называются вариометрами). При какой магнитной связи в цепи наступит резонанс напряжений?
Р е ш е н и е. Из условия резонанса напряжений (2.33) находим индуктивность цепи при резонансе:
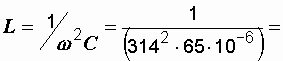 0,156 Гн.
0,156 Гн.
При согласном включении катушек их общая индуктивность равна 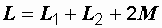 , отсюда
, отсюда 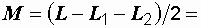 (0,156–0,04–0,09)/2 = 0,026 Гн.
(0,156–0,04–0,09)/2 = 0,026 Гн.
Коэффициент магнитной связи 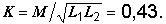
Дата добавления: 2015-01-29; просмотров: 1385;
