Чистая приведенная стоимость (NPV)
Основополагающим принципом инвестиционного анализа является принцип временной ценности денег, который гласит:
Денежные суммы, относящиеся к разным периодам времени, имеют разную ценность, и поэтому суммировать или сравнивать разновременные денежные суммы можно только после того, как все они приведены к определенному моменту времени.
Суть этого принципа заключается в том, что в условиях рыночной экономики «время порождает деньги». Сумма денег, вложенная в то или иное дело, через некоторое время прирастает на величину дохода, зависящего от нормы доходности и продолжительности временного периода. Поэтому денежная сумма ценится тем больше, чем к более раннему периоду она относится, т.е. чем раньше она может принести новый доход.
Пусть r – заданная годовая норма доходности (в долях единицы). Сначала допустим, что это – ставка процента по банковскому депозиту. Тогда некоторая сумма C0, будучи положенной на банковский депозит на условиях сложных процентов, через год увеличится до (1+ r) C0, а через t лет – до (1+ r)t C0.
Теперь предположим, что Вы имеете возможность поместить ту же сумму C0 в дело, которое через t лет принесет разовый (безрисковый) доход в размере C. Понятно, что Вы предпочтете этот проект простому размещению средств на банковском депозите, если будет выполняться условие:
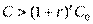
или же
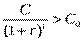
Экономическая суть последнего неравенства заключается в том, что сумма C, относящаяся к периоду t, предварительно приводится (дисконтируется) к начальному моменту времени посредством величины 1/(1 + r)t, называемой дисконтным множителем. При этом величина r называется ставкой дисконтирования.
Разумеется, в подобных сравнениях в качестве r может браться не только ставка процента по депозиту, но и любая другая достижимая норма доходности (для данного инвестора).
Теперь вспомним, что инвестиционный проект в общем случае предполагает не одно, а множество возвратных денежных поступлений в течение периода действия проекта. В таких ситуациях уже все предполагаемые денежные поступления сначала приводятся к начальному периоду времени, а затем суммируются. Результатом является приведенная стоимость (Present Value – PV) возвратного денежного потока данного проекта:
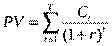 (1)
(1)
Учитывая, что в начале инвестиционного проекта возникает отток денежных средств в размере C0, приходим к основному показателю инвестиционного проекта – чистой приведенной стоимости (Net Present Value – NPV):
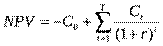 (2)
(2)
Данный показатель считается наиболее подходящим для отбора инвестиционных проектов. Общее правило состоит в следующем:
Проект можно принять, если NPV больше нуля, а среди нескольких таких проектов следует выбирать тот, у которого этот показатель принимает максимальное значение.
Вернемся к примеру из пункта 1. Понятно, что при любом значении r > 0 величина NPV проекта 1 окажется выше, чем проекта 2, и значит, проект 1 является всегда более предпочтительным.
Вопрос о том, следует ли принять проект 1, зависит от ставки дисконтирования r. Предположим, что выбрана ставка r = 0,10 (10%). Тогда получается следующий расчет:
| Год 0 | Год 1 | Год 2 | Год 3 | Всего | |
| Денежный поток | –1 000 | ||||
| Дисконтный множитель | 0,909 | 0,826 | 0,751 | ||
| Чистая приведенная стоимость | –1 000 |
В данном случае NPV = 11 > 0, и значит, проект 1 можно принять. Но если имеется альтернативный вариант инвестиционных вложений с нормой доходности r = 0,11 (11%), то окажется (как легко проверить), что NPV = – 6, и значит, этот проект нужно уже отвергнуть.
Что касается проекта 2, то для него при r = 0,10 имеем NPV = – 21, и, значит, проект при требуемом уровне доходности надо отвергнуть, даже если бы это было единственное инвестиционное предложение.
Дата добавления: 2015-01-29; просмотров: 907;
