Расчет осей и валов на выносливость

При расчете вращающихся осей и валов на выносливость учитывают все основные факторы, влияющие на усталостную прочность: характер изменения напряжений, статические и усталостные характеристики материалов, изменение предела выносливости вследствие концентрации напряжений и влияние абсолютных размеров осей или валов, состояние поверхности. Для учета всех этих факторов конструкция вала должна быть известна.

Расчет осей и валов на выносливость заключается в том, что для каждого опасного сечения определяют действительный коэффициент запаса усталостной прочности «n» и сравнивают его с допускаемым [n]. Следовательно, расчет вала на выносливость осуществляют как проверочный.

Оси

Неподвижная ось, напряжения в которой изменяются по нулевому циклу (σ_а = σ_m):

.

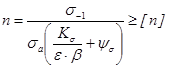Вращающаяся ось напряжения в которой соответствуют симметричному циклу

.

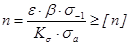При сложном напряженном состоянии и любых циклах изменения напряжений действительный коэффициент запаса прочности «n» равен

,

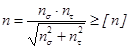где n_σ – коэффициент запаса прочности по нормальным напряжениям изгиба;

n_τ – коэффициент запаса прочности по касательным напряжениям кручения.

Значения этих коэффициентов определяют по формулам:

при изгибе

,

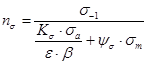при кручении

.

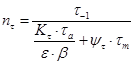При расчете принимают, что нормальные напряжения изменяются по симметричному циклу 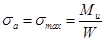, σ_m= 0,

а касательные – по пульсирующему отнулевому циклу

.

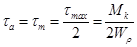Реверсивный вал работает на чистое кручение

,

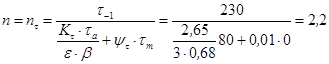σ_а и τ_а – амплитудное значение напряжений при знакопеременном симметричном цикле ,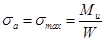

при отнулевом ,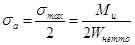

σ_m и τ_m­ – среднее напряжение цикла, при симметричном, знакопеременном цикле σ_m = 0,

при общенулевом цикле ,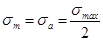

где σ_-1 и τ_-1 – пределы выносливости соответственно при изгибе и при кручении для симметричного цикла изменения напряжений.

Для стали при изгибе σ_-1 = (0,4…-,45)σ_β

при кручении τ_-1 = 0,2 σ_β,

σ_а и τ_а – амплитуды циклов при изгибе и кручении.

Можно считать, что нормальные напряжения, возникающие в напряженном сечении вала от изгиба, изменяются по симметричному циклу

, .

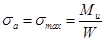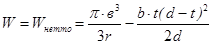Так как величина момента, передаваемого валом является переменной, то при расчете принимают для касательных напряжений наиболее неблагоприятный знакопеременный

цикл – отнулевой (пульсирующий цикл), тогда

,

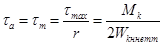где σ_m и τ_m – средние напряжения циклов при изгибе и кручении.

Кσ и Кτ – эффективные коэффициенты концентрации напряжений при изгибе и кручении.

W_нетто – момент сопротивления сечения вала с учетом шпоночной канавки.

При изгибе .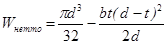

При кручении .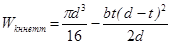

В зависимости от фактора концентрации: галтель, кольцевая выточка (канавка), поперечное отверстие, шпоночная канавка, шлицы, резьба, прессовая посадка и состояния поверхности (вид обработки) значения коэффициентов Кσ и Кτ принимают по таблицам.

При действии в одном и том же сечении вала нескольких факторов концентрации напряжений от формы, учитывают наиболее опасный их них, а общий эффективный коэффициент концентрации напряжений от формы и состояния поверхности определяют по формуле:

При изгибе К_σ = К_σФ + К_σП – 1

При кручении К_τ = К_τФ + К_τП – 1,

где К_σФ и К_τФ – эффективные коэффициенты концентрации от формы.

К_τФ и К_τП – эффективные коэффициенты концентрации от состояния поверхности

ε – масштабный фактор – коэффициент, учитывающий влияние размеров сечения вала на его прочность. Значения ε определяют по таблицам в зависимости от вида деформации и диаметра вала.

β – коэффициент упрощения, характеризующий повышение предела выносливости в зависимости от вида поверхностной обработки вала (термообработка, дробеструйный наклеп, накатка роликами). Выбирается β (1,1…2) выбирается по таблицам.

ψ_σ и ψ_τ – коэффициенты, учитывающие влияние асимметрии цикла напряжений на прочность вала при изгибе и кручении. Их значения находят из таблицы в зависимости от величины σ_β материала вала.

Допускаемый коэффициент запаса усталостной прочности [n] принимают в зависимости от назначения вала и точности расчетов.

[n] = 1,5…2,5.

Если диаметры валов определяются условиями жесткости, то значения [n] могут быть значительно выше.

При точном определении расчетных нагрузок, точных расчетах, однородном материале вала

[n]_min = 1,3.

Различают изгибную и крутительную жесткость валов.