Динамика ременной передачи

Если пренебречь влиянием веса, то на ременную передачу в состоянии покоя действует сила предварительного напряжения (S₀). На обеих ветвях усилие S₀ одинаково.

Кроме того, зная σ₀ = 18 МПа, можно также определить S₀.

S₀ = σ₀ F = σ₀ ·b·h

При холостом ходе и малой скорости передачи усилия на обеих ветвях одинаковы и соответствуют предварительному натяжению:

S₁ = S₂ = S₀

Чтобы передать окружное усилие (P) натяжение ветвей должно быть различно на величину (P):

S₁ – S₂ = P (10.1)

Увеличение натяжения одной ветви приводит к соответствующему уменьшению натяжению другой, в то время как сумма натяжений сохраняется постоянной:

S₁ + S₂ = 2S₀ (10.2)

т.е. сумма натяжений ветвей ремня при рабочем ходе (S₁ + S₂) равна сумме свободных натяжений ветвей при холостом ходе (S₀ + S₀) или состоянии покоя. Это соотношение не вполне подтверждается опытом:

S₁ + S₂ > 2S₀ ≠ const;

и с увеличением окружной скорости ремня возрастает. Из совместного решения уравнений (10.1) и (10.2) найдем:

;

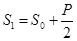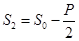
Усилие предварительного натяжения S₀ во время работы передачи рассматривается как среднее натяжение ветвей ремня, т.е.

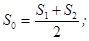
Непосредственную связь между натяжением ветвей ремня можно также выразить аналитической зависимостью, установленной Л. Эйлером в 1775 г.

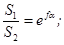(10.3)

e – основание натурального логарифма, e = 2,7182818284

Формула Эйлера выведена для гибкой нерастяжимой и невесомой нити, скользящей по неподвижному цилиндру. Реальная ременная передача отличается от условий, принятых Эйлером. Поэтому формула (10.3) дает лишь приближенную зависимость и степень приближения зависит от достоверности значений коэффициента (f), под которым понимается приведенный коэффициент трения по всей дуге обхвата (α) (средние значения “f” находят из таблиц).

Для определения полных усилий S₁ и S₂ надо учесть центробежное воздействие С, вызывающее в ветвях ремня дополнительно растягивающую силу.

С = ρ·А·V² (10.4)

где: ρ – плотность ремня

V – скорость ремня в м/с;

Таким образом, натяжение в ветвях при работе передачи будет равно: S₁ + C; S₂ + C и при холостом ходе S₀ + C.

Из формулы (10.4) ясно, натяжение C, возникающее от действия центробежных сил, не зависит от радиуса кривизны элемента ремня и для всех его частей одинаково. Центробежные силы инерции вызывают в ремне растягивающие напряжения.