Расчет передач по кривым скольжения

Кривые скольжения для приведенных ремней получены опытным путем группой инженеров ЦНИИТМАШ.

При этом ставится цель: обеспечить необходимые тяговые свойства ремня (отсутствие буксования и неспокойного хода ремня) и высокий КПД передачи. При этом методе расчета напряжения в ремне получаются меньше допускаемых. При этом обеспечиваются и тяговые свойства ремня и достаточная его прочность. Кривые скольжения получают экспериментально: при постоянном натяжении S₀ постепенно повышают полезную нагрузку P и измеряют скольжение S. При этом вводится понятие о коэффициенте тяги φ.

Относительное скольжение равно

;

где: n₂ и 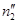– частоты вращения ведомого шкива соответственно на холостом ходу и под нагрузкой.

Отношение передаваемого ремнем окружного усилия к сумме натяжений его ветвей называется коэффициентом тяги.

;

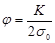
K – полезное напряжение в ремне.

В координатах S–φ строится кривая тяговой характеристики ременной передачи (рис. 10.8). Прямолинейный участок, где с ростом φ прямо пропорционально растет S называется рабочим участком. Второй участок криволинейный, отражающий неустойчивую работу ремня (пробуксовки и полное буксование) называется нерабочим.

Рис. 10.8. Кривая скольжения ремня

Точка перехода от прямолинейного участка к криволинейному называется критической точкой тяговой характеристики. Кривые скольжения и КПД показывают, что оптимальная нагрузка ременных передач лежит в зоне критических значений коэффициента тяги (φ₀), наиболее высокий КПД.

При φ < φ₀ тяговая способность ремня не используется полностью, при φ > φ₀ ремень работает неустойчиво и быстро изнашивается. На основании многочисленных исследований можно рекомендовать для плоских ремней:

кожаных и прорезиненных – φ₀ ≈ 0,6;

хлопчатобумажных и льняных – φ₀ ≈ 0,5;

шерстяных – φ₀ ≈ 0,4;

полиамидных – φ₀ ≈ 0,45…0,5.

Численные значения коэффициента тяги “φ” зависят от вида ремня, его толщины, диаметра шкивов, скорости и т.д. Однако характер кривой скольжения остается постоянным при любой комбинации перечисленных параметров. Это положение позволило установить общие нормы работоспособности ремня с учетом влияния различных параметров. Так, условия работы ременной передачи считаются нормальными, если

;

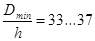здесь D_min – наименьший диаметр шкива,

h – толщина ремня,

σ₀ – допустимое полезное напряжение.

е) Допускаемое полезное напряжение

Полезное напряжение, соответствующее коэффициенту тяги φ будет равно:

К₀ = 2·σ₀·φ₀.

В таблицах приводятся значения “K₀” для различных ремней при разном соотношении h/D_min и в этом случае уже “K₀” принимается как критическое полезное напряжение “К₀”. Но табличные значения “K₀” получены при определенных условиях (передача открытая, α =180⁰; v =10 м/с). В действительности условия отличаются от этих поэтому расчет передачи следует вести не по “K₀”, а по напряжению σ_П, с учетом поправочных коэффициентов:

σ_П = К₀ С,

где С = С₀ ·Сh·Cα·Cv,

здесь: С₀ – коэффициент, учитывающий условия натяжения ремня и расположение передачи в пространстве.

С_h – коэффициент, учитывающий влияние отношения h/D_min

для прорезиненных ;

для кожаных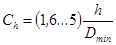

Cα – коэффициент, учитывающий влияние угла обхвата.

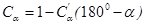
Для плоских ремней ;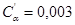

C_v – скоростной коэффициент, учитывающий ослабление сцепления ремня со шкивом под действием центробежной силы. Для передач с автоматическим регулированием натяжение ремня C_v = 1.

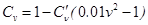
Для плоских среднескоростных ремней из традиционных материалов 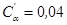и т.д.

Величина σ_п необходима, например, при расчете параметров ремня.

, см²,

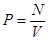где Н;

b – ширина ремня

или ;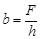

h – ширина ремня, которой задаются, соблюдая соотношение D_min/h.