Расчетные формулы каскада в области средних частот.
Заменив Ег на mUвх и Rг на внутреннее сопротивление полевого транзисторав точке покоя Riт.п,из эквивалентной схемы для средних частот (см. рис. 2.4.5 б) нетрудно найти коэффициент усиления напряжения резисторного каскада с полевым транзистором К, равный отношению выходного напряжения каскада к входному в области средних частот:
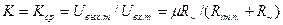 . (2.4.5)
. (2.4.5)
Для полевых транзисторов полученное выражение неудобно, так как m у них очень сильно зависит от положения рабочей точки и найти его трудно; заменив в (2.4.5) m на Sт.пRiт.п, где Sт.п — статическая крутизна характеристики тока стока в точке покоя, получим:
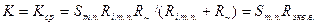 , (2.4.6)
, (2.4.6)
где Rэкв.в — сопротивление эквивалентного генератора на верхних частотах и, как показано выше, равное параллельному соединению Ri.е.пR~, а следовательно, параллельному соединению Riт.п, R и R0. Так как в каскадах с полевыми транзисторами Riт.п>>R~, то в знаменателе формулы (2.4.6) можно пренебречь величиной R~ по сравнению с Riт.п и получить:
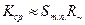 . (2.4.7)
. (2.4.7)
Этим выражением обычно и пользуются для расчета коэффициента усиления резисторных каскадов с полевыми транзисторами, так как определение статической крутизны характеристики Sт..п в точке покоя графически затруднений не представляет.
Коэффициент усиления промежуточных широкополосных каскадов с полевыми транзисторами рассчитывают по еще более простой формуле:
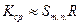 (2.4.8)
(2.4.8)
При расчете каскадов с биполярными транзисторами обычно пользуются не коэффициентом усиления напряжения, а коэффициентом усиления тока Кт, представляющим собой отношение тока сигнала в базе следующего каскада IБтсл к току сигнала IБт в цепи базы рассчитываемого каскада (см. рис. 2.4.1а):

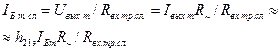 (2.4.9)
(2.4.9)
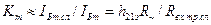
где Rвх.тр.сл — входное сопротивление транзистора следующего каскаде, a R~ — сопротивление нагрузки цепи коллектора рассчитываемого каскада для тока сигнала, равное согласно формуле (2.4.3) параллельному соединению R, Rвх.тр.сл и Rд.сл.
Если требуется определить коэффициент усиления напряжения резисторного каскада с биполярным транзистором, то достаточно поделить Uвых.т на Uвх.т=Iвх.тRвх.тр или помножить Кт на отношение входных сопротивлений каскадов:
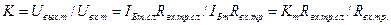 (2.4.10)
(2.4.10)
Из эквивалентной схемы для нижних частот, изображенной на рис. 2.4.5а, находят уравнение частотной характеристики резисторных каскадов для этих частот, представляющее собой зависимость относительного усиления Y от частоты сигнала, или обратную зависимость коэффициента частотных искажений M=1/Y от частоты:
 ; (2.4.11)
; (2.4.11)
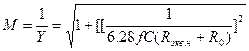 . (2.4.12)
. (2.4.12)
Здесь f — частота, на которой определяют относительное усиление или коэффициент частотных искажений; Rэкв.н и R0 определены ранее для каскадов при анализе эквивалентной схемы на низших частотах.
Выражение (2.4.11) показывает, что относительное усиление Y резисторного каскада на низших частотах изменяется от 0 до 1 при изменении частоты сигнала от 0 до ∞.
Положив в (2.4.12) М=Мн, f = fн и решив результат относительно С, получим формулу для расчета необходимой емкости конденсатора межкаскадной связи по допустимому коэффициенту частотных искажений Мн на низшей рабочей частоте fн:
 . (2.4.13)
. (2.4.13)
Уравнение частотной характеристики для области высших частот рабочего диапазона транзисторного и лампового резисторных каскадов, представляющее собой зависимость относительного усиления Y от частоты, а также обратную зависимость коэффициента частотных искажений М=1/Y от частоты, находят из эквивалентной схемы резисторного каскада для высших частот, изображенной на рис. 2.4.5в.
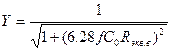 ; (2.4.14)
; (2.4.14)
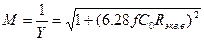 . (2.4.15)
. (2.4.15)
Сопротивление Rэкв.в на основании сказанного ранее для лампового резисторного каскада представляет собой параллельное соединение Ri, R и Rgсл:


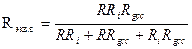 ;
;

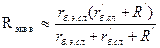 , (2.4.16)
, (2.4.16)
а во второй формуле (2.4.16) относящейся к транзисторному резисторному каскаду, работающему на биполярный транзистор, для которого почти всегда Rr>>R:
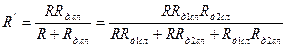 .
.
Из-за влияния rб.сл, входящего в эквивалентную схему рис. 2.4.3а, свойства и характеристики резисторных каскадов, работающих на входную цепь биполярного транзистора, сильно отличаются на очень высоких частотах от свойств и характеристик резисторных каскадов, работающих на вход полевого транзистора; на высоких частотах rб.сл уменьшается и превращается в rб, входящее в выражение (2.4.16).
Выражение (2.4.14) показывает, что относительное усиление резисторного каскада на верхних частотах изменяется от 1 до 0 приизменении частоты сигнала от 0 (средние частоты) до ∞
Решив выражение (2.4.15) относительно Rэкв.в, получим формулу, позволяющую найти по заданной верхней рабочей частоте fв и коэффициенту частотных искажений Мв на этой частоте:
 (2.4.17)
(2.4.17)
По найденному значению Rэкв.вmax, используя соотношения (2.4.4) и (2.4.16), для достаточно высокочастотного транзистора следующего каскада можно выбрать сопротивления резисторов схемы, обеспечивающие удовлетворение предъявленных к каскаду требований.
Вид фазовой характеристики резисторного каскада, изображенной на рис. 2.4.4 б, нетрудно пояснить по эквивалентным схемам рис. 2.4.5. Так, из эквивалентной схемы рис. 2.4.5 а видно, что на нижних частотах сопротивление цепи, подключенной к генератору сигнала, имеет емкостную и активную составляющие, а поэтому ток сигнала I в цепи опережает ЭДС эквивалентного генератора на угол φ, стремящийся к 90° при безграничном понижении частоты. Выходное напряжение резисторного каскада Uвых, равное произведению этого тока на R0, также будет опережать ЭДС, а следовательно, и находящееся с ней в фазе входное напряжение на тот же угол. На верхних частотах, как видно из рис. 2.4.5 в, ток в цепи также опережает ЭДС эквивалентного генератора на угол, меньший 90°, так как цепь имеет активную и емкостную составляющие сопротивления. Но выходное напряжение, представляющее собой падение напряжения сигнала на емкости С0, отстает на 90° от тока сигнала через эту емкость, а следовательно, отстает от ЭДС эквивалентного генератора, находящегося в фазе с ЭДС. В результате в области верхних частот у резисторного каскада угол сдвига фазы φ между выходным и входным напряжениями при безграничном повышении частоты стремится к 90°. Фазовая характеристика как транзисторного каскада на биполярном транзисторе, так и транзисторного каскада на полевом транзисторе в области нижних и верхних частот (соответствующая эквивалентным схемам рис.2.4.5)
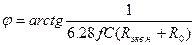 ;
;
 . (2.4.18)
. (2.4.18)
Отрицательное значение угла сдвига фазы в последней формуле свидетельствует о том, что на верхних частотах выходное напряжение отстает от входного.
На рис. 2.4.6в показано, как искажается форма прямоугольного импульса, усиливаемого резисторным каскадом; рассмотрим физические основы возникновения этих искажений, называемых переходными.
При подаче мгновенного скачка напряжения на вход резисторного каскада емкости С и С0 от воздействия этого скачка заряжаются. Процесс заряда малой емкости С0 происходит быстро, и напряжение на ней, являющееся выходным напряжением каскада, достигает установившегося значения через очень малый промежуток времени (рис. 2.4.6а); заряд этой емкости, а следовательно, и нарастание выходного напряжения происходят по экспоненциальному закону. За это время разделительный конденсатор С, имеющий большую емкость, не успевает заметно зарядиться, и напряжение на нем в процессе заряда емкости С0 можно считать равным нулю. Поэтому при рассмотрении процесса нарастания фронта выходного импульса в эквивалентной схеме каскада можно закоротить С, исключив тем самым его из схемы; при этом эквивалентная схема каскада превращается в эквивалентную схему для верхних частот.

Рис. 2.4.6. Переходные характеристики резисторного каскада:
а — в области малых времен; б, — в области больших времен; в — искажения одиночного прямоугольного импульса
По мере заряда конденсатора С выходное напряжение резисторного каскада, равное разности напряжения скачка между точками М и Н (см. рис. 2.4.3 б) и напряжения на конденсаторе С, уменьшается, вследствие чего переходная характеристика каскада в области больших времен экспоненциально падает при увеличении времени (рис. 2.4.6 б). Так как заряд конденсатора С занимает много большее время, чем заряд емкости С0, то при рассмотрении процесса заряда конденсатора С емкость С0 можно считать уже заряженной и удалить ее из схемы; в этом случае схема превратится в эквивалентную схему для нижних частот. Отсюда следует, что переходная характеристика каскада в области малых времен, определяющая его время установления и обусловленная в резисторном каскаде процессом заряда емкости С0, определяется эквивалентной схемой каскада для верхних частот, а переходная характеристика каскада в области больших времен, определяющая искажения вершины усиливаемых импульсов и обусловленная в резисторном каскаде процессом заряда разделительного конденсатора С, определяется эквивалентной схемой каскада для нижних частот.
Из того, что переходная характеристика резисторного каскада в области больших и малых времен определяется теми же эквивалентными схемами для нижних и верхних частот, что и частотная и фазовая характеристики, следует:
1) частотная и фазовая характеристики каскада на верхних частотах определяют его переходную характеристику в области малых времен, а следовательно, его время установления и выброс;
2) частотная и фазовая характеристики каскада на нижних частотах определяют его переходную характеристику в области больших времен, а следовательно, и искажения вершины импульсов;
3) частотная и фазовая характеристики усилительного каскада жестко связаны с его переходными характеристиками.
Эти правила справедливы для каскадов с любой схемой межкаскадной связи.
Из-за искажений, вносимых емкостью С0 и конденсатором С, одиночный прямоугольный импульс, прошедший через резисторный каскад, приобретает вид, показанный на рис. 2.4.6в.
Переходная характеристика в области больших времен, определяемая процессом заряда конденсатора С через сопротивления Rэкв.н+R0 и представляющая собой монотонно падающую по экспоненциальному закону кривую (рис. 2.4.6 б), стремится к нулю при неограниченном возрастании времени t и определяется уравнением:
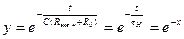 , (2.4.19)
, (2.4.19)
где 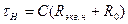 , (2.4.20)
, (2.4.20)
представляет собой постоянную времени резисторного каскада на нижних частотах, а
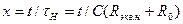 , (2.4.21)
, (2.4.21)
является нормированным временем. Приравняв в (2.4.19) время t длительности импульса Ти, найдем, что спад вершины прямоугольного импульса, вносимый резисторным каскадом
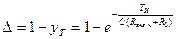 . (2.4.22)
. (2.4.22)
Положив в (2.5.22) 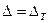 и решив результат относительно С, получим формулу для расчета емкости конденсатора межкаскадной связи по допустимому спаду вершины Дт прямоугольного импульса длительностью Т:
и решив результат относительно С, получим формулу для расчета емкости конденсатора межкаскадной связи по допустимому спаду вершины Дт прямоугольного импульса длительностью Т:
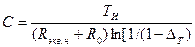 .
.
При ΔТ<<1, что обычно имеет место на практике, ln1/(1- ΔТ)~ ΔТ и формула для расчета необходимой емкости конденсатора С упрощается:
 . (2.4.23)
. (2.4.23)
Выражение (2.4.23) дает немного завышенное значение С, но это завышение даже при ΔТ=0,1 составляет всего лишь около 5%, что допустимо. Решив (2.4.23) относительно ΔТ, получим 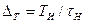 , откуда следует, что спад приближенно равен отношению длительности импульса к постоянной времени каскада на нижних частотах. Например, для получения спада 2% при длительности импульса 2 ,мс необходима постоянная времени каскада, в 50 раз превышающая длительность импульса и, следовательно, равная 0,1 с.
, откуда следует, что спад приближенно равен отношению длительности импульса к постоянной времени каскада на нижних частотах. Например, для получения спада 2% при длительности импульса 2 ,мс необходима постоянная времени каскада, в 50 раз превышающая длительность импульса и, следовательно, равная 0,1 с.
Переходная характеристика в области малых времен, определяемая процессом заряда паразитной емкости С0 и представляющая собой кривую, изображенную на рис. 2.4.6 а, определяется уравнением
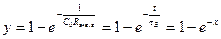 , (2.4.24)
, (2.4.24)
где 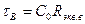 . (2.4.25)
. (2.4.25)
есть постоянная времени резисторного каскада на верхних частотах, а
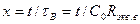 . (2.4.26)
. (2.4.26)
представляет собой нормированное время.
Как видно из уравнения (2.4.24), процесс установления фронта импульса на выходе резисторного каскада происходит монотонно, а следовательно, у резисторного каскада выброс фронта отсутствует.
Нормированное время установления резисторного каскада ху нетрудно найти из уравнения (2.4.24), определив из него х1, соответствующий значению y1 = 0,1, и х2, соответствующий y2 = 0,9:
y1=0,1= 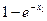 ; x1=ln1,11; y2=0,9=
; x1=ln1,11; y2=0,9=  ; x2=ln10.
; x2=ln10.
Отсюда:
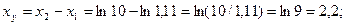
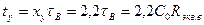 . (2.4.27)
. (2.4.27)
Решив уравнение (2.4.27) относительно Rэкв.в, получим формулу, позволяющую найти необходимое значение Rэкв.вmax по заданному времени установления каскада:
 . (2.4.28)
. (2.4.28)
Используя соотношения (2.4.4) и (2.4.16) для достаточно высокочастотного транзистора следующего каскада по известному Rэкв.вmax, можно выбрать сопротивление резисторов схемы, обеспечивающее удовлетворение предъявленных к каскаду требований.
Положив в уравнении (2.4.14) частоту f равной верхней граничной частоте резисторного каскада fв.гр, на которой относительное усиление Yв.гр=0,707, и решив это уравнение совместно с (2.4.27), найдем соотношение между fв.гp и ty:
 ;
;  . (2.4.29)
. (2.4.29)
Зная верхнюю граничную частоту, по формулам (2.4.29) можно найти время установления (и наоборот); соотношения (2.4.29) приближенно справедливы для любых усилительных каскадов и даже для многокаскадных усилителей.
Дата добавления: 2015-01-09; просмотров: 1785;
