Часть 2. Рассмотрение ПШ последовательностей в частотной области

1. Остановите и сверните осциллограф.

2. Запустите и настройте NI ELVIS II Dynamic Signal Analyzer VI.

Input Settings:

- Source Channel Scope CH0; Voltage Range ±10V

FFT Settings:

- Frequency Span 40000; Resolution 400; Window 7 Term B-Harris

Averaging:

- Mode RMS; Weighting Exponential; # of averages 3

Trigger Settings:

- Type Digital

Frequency Display:

- Units dB; Mode RMS; Scale Auto.

Правильно настроенное окно должно выглядеть так:

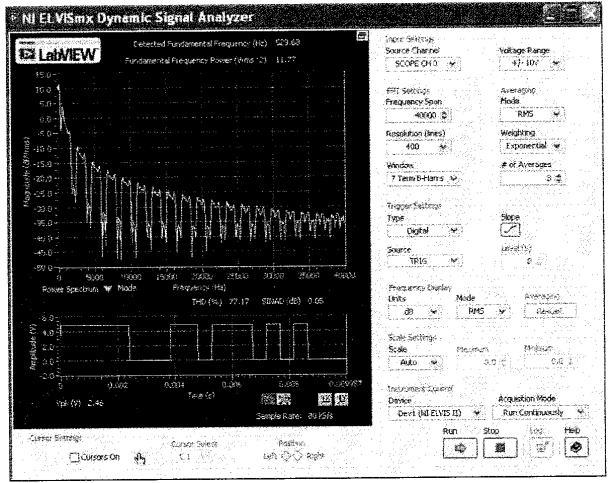
Рисунок 14.8

3. Определите частоту первого нуля для 31-битной последовательности. После этого сравните свои расчеты с результатом, полученным на экране анализатора сигналов.

4. Сколько гармоник теоретически присутствует в одной доле спектра последовательности X? Почему мы не можем видеть каждую из них? Чтобы проверить свой ответ, установите Frequency Span на 2,500кГц. Как только экран обновится, вы должны увидеть набор отдельных гармоник первой доли сигнала. Посчитайте точное количество гармоник от 0 до 2,083кГц и сравните со своими расчетами.

5. Заново настройте Dynamic Signal Analyzer:

Input Settings:

- Source Channel Scope CH0

FFT Settings:

- Frequency Span 40000

Теперь мы рассматриваем последовательность, состоящую из 255 бит.

5. Повторите пункты 3 и 4 для более длинной последовательности. Можете ли вы на экране анализатора сигналов различить все гармоники одной доли спектра последовательности? Уменьшайте Frequency Span ниже 2,500кГц и попытайтесь рассмотреть отдельные гармоники. У какой из последовательностей плотность гармоник выше?

Часть 3. Использование ПШ последовательностей для генерации шума

Теоретически, генерация белого шума невозможна. Объясняется это тем, что бесконечное количество гармоник с равным распределением энергетической плотности требует бесконечного количества энергии. В то же время, как вы могли видеть в предыдущей части эксперимента, длинная ПШ последовательность имеет большое количество гармоник, и более того, некоторые участки ее спектра имеют довольно плоскую форму. Исходя из этого, можно изолировать часть спектра ПШ последовательности с помощью фильтра и смоделировать белый шум с ограниченной полосой.

1. Остановите Signal Analyzer VI. Полностью разберите собранную схему.

2. Запустите NI ELVIS II Function Generator VI. Установите частоту сигнала 150кГц.

3. Соберите схему, показанную на рисунке 14.9.

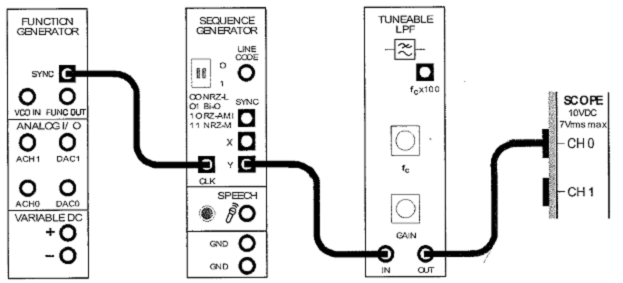
Рисунок 14.9

Схеме соответствует блок-схема на рисунке 10. Математические расчеты говорят о том, что при частоте 150кГц и 255 гармониках на одну долю спектра последовательности гармоники отстоят друг от друга на 588Гц.

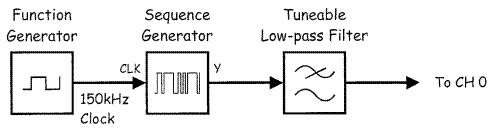
Рисунок 14.10

4. Установите регулятор Gain модуля Tuneable Low-pass Filter в среднее положение, а Cut-off Frequency Adjust – в крайнее правое. Частота среза фильтра нижних частот установлена на 15 кГц.

5. Запустите осциллограф. Настройте его:

- Timebase 1ms/div

- Trigger Type Immediate

- CH 1 выключен

6. На что похож сигнал на выходе фильтра низких частот?

Сигнал на выходе ФНЧ не «белый» шум, потому что имеет ограниченный спектр. Не является это сигнал и «шумом». Настоящий шум не повторяется, в то время как сигнал на выходе ФНЧ повторяется каждые 1,7мс. Повторяющуюся природу сигнала можно рассмотреть с помощью осциллографа.

7. Остановите осциллограф, чтобы сигнал на его экране можно было рассмотреть. Внимательно посмотрите на сигнал – вы должны увидеть примерно пять его повторений. Измерьте период повторения сигнала. Посчитайте, сколько гармоник пропускает ФНЧ?

8. Запустите Signal Analyzer со следующими настройками:

- Source Channel Scope CH 0

- Frequency Span 20,000Hz

- Trigger Type Immediate

9. На экране анализатора сигналов определите число гармоник, присутствующих между частотой 0Гц и частотой среза.

10. Остановите Signal Analyzer и запустите осциллограф.

11. Измените схему, как показано на рисунке 14.11.

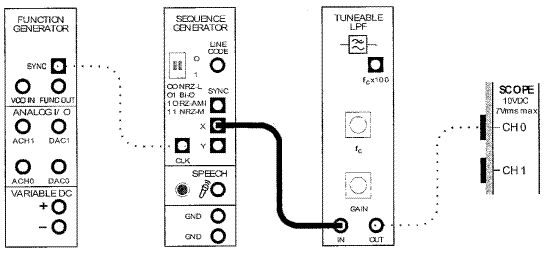
Рисунок 14.11

12. Рассмотрите сигнал на выходе ФНЧ. Почему он больше не выглядит как электрический шум?

Чтобы получить ответ на этот вопрос, закройте осциллограф и вновь запустите анализатор сигналов. Посчитайте число гармоник между 0Гц и частотой среза.