Теоретическая часть. Рисунок 13.1 показывает пример возможного ЧМн сигнала.

Рисунок 13.1 показывает пример возможного ЧМн сигнала.

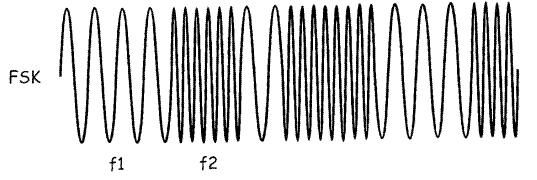
Рисунок 13.1

На рисунке 13.1 сигнал выглядит так, как будто состоит из всего двух частот – f1 и f2. Это предполагает, что в частотной области он должен выглядеть, как на рисунке 13.2а. Несмотря на очевидность, ни одно из этих предположений не является верным.

В моменты, когда цифровой сигнал меняет состояние, переключение между частотами f1 и f2 делает ЧМн сигнал более сложным, чем просто две синусоиды. Более того, ширина сигнала гораздо больше, чем просто разница между двумя этими частотами. Определение полосы частот ЧМн сигнала – очень сложная задача, поэтому на рисунке 13.2б представлена упрощенная спектральная композиция сигнала.

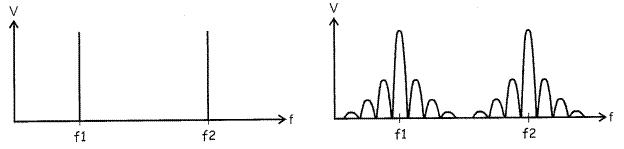
Рисунок 13.2а Рисунок 13.2б

Одно из важнейших требований, предъявляемых к схемам модуляции, это ширина полосы частот модулированного сигнала. Новые приложения и программы разрабатываются каждый день, и всем им необходим доступ к радиочастотному спектру. Но радиочастотный спектр – ограниченный ресурс. Поэтому важно, чтобы занимаемая модулированным сигналом полоса частот была как можно меньше, при этом сохраняя качество связи. Это позволит большему количеству потенциальных пользователей использовать определенный спектр частот.

Вариант частотной манипуляции, разработанный специально для уменьшения ширины спектра сигнала – это Гауссовская Частотная Манипуляция (GFSK). GFSK используется в технологиях Bluetooth, DECT, GSM и других, при этом являясь той же самой частотной манипуляцией (FSK), но с одним отличием – цифровой сигнал перед модуляцией сначала пропускается через фильтр нижних частот с гауссовской импульсной характеристикой.

Применение гауссовского фильтра является наилучшим компромиссом между подавлением боковых лепестков в спектре модулированного сигнала и вносимыми интермодуляционными искажениями. Гауссовский сглаживающий фильтр приводит к исключению резких переходов от одного отрезка синусоиды к другому, как это характерно для обычного ЧМн сигнала. Сглаживание импульсов выражается в «затягивании», когда импульс существует не на конечном символьном интервале, а распространяется на соседние. Распространение каждого символа на соседние временные интервалы исключает возможность резкого изменения формы модулирующего сигнала а, следовательно, и модулируемого параметра.