Обследования

Если бы все, ответившие «да» на 1-й вопрос, отвечали бы «да» на 2-й вопрос, и так же совпадали ответы «нет», то связь была бы предельно тесной, функциональной. Но на самим деле распределение ответов на оба вопроса не совпадает. Большая часть ответивших «да» на 1-й вопрос ответила «да» и на 2-й вопрос, но часть ответила «нет». То же относится к ответившим «да» на 2-й вопрос. Связь есть, но неполная, типа корреляционной, и нужно измерить тесноту этой связи.

К. Пирсон предложил показатель, названный коэффициентом ассоциации. В числителе этого относительного показателя разность произведения чисел с одинаковыми ответами на оба вопроса: да-да и нет-нет и произведения чисел с неодинаковыми ответами: да-нет И нет-да. В знаменателе коэффициента ассоциации - корень квадратный из произведения всех четырех частных итогов. В буквенных обозначениях по табл. 8.13 имеем:

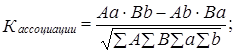(8.48)

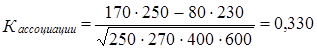
Свойства коэффициента ассоциации такие же, как и у коэффициента корреляции: коэффициент ассоциации обращается в нуль, если оба произведения в числителе точно уравновешиваются (что крайне маловероятно); он равен плюсединице, если отсутствуют оба гетерогенных сочетания Аb и Ba; равен минус единице, если отсутствуют гомогенные сочетания ответов Аа и Bb.

Другой метод измерения связи по «четырехклеточной таблице» предложен английскими статистиками Эдни Дж. Юлом (1871-1951) и Морисом Дж. Кендэлом (1907). Числитель этого коэффициента, называемого коэффициентам контингенции, совпадает с числителем коэффициента ассоциации Пирсона, а в знаменателе - сумма тех же произведений, разность которых стоит в числителе:

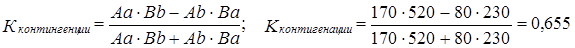
Как видим, коэффициент Юла-Кендэла значительно выше, чем коэффициент Пирсона. Крупный недостаток данного коэффициента в том, что уже при равенстве нулю только одного из двух гетерогенных сочетаний - либо Аb, либо Bа коэффициент Юла - Кендэла обращается в единицу. Можно сказать, что этот показатель очень либерально оценивает тесноту связи, завышает ее.

Наконец, вполне возможно предложить показатель тесноты связи в форме отношения избытка суммы гомогенных сочетаний над их пропорциональной суммой к предельно возможному избытку.

Для этого необходимо вначале вычислить, каковы были бы пропорциональные числа гомогенных сочетаний Аа и Bb? Пропорциональные числа - это доли от общей численности совокупности «N», которые были бы получены при полном отсутствии взаимосвязи группировок по двум признакам (ответам на два вопроса), т. е. числа (SA·Sa:N) и (SB·Sb:N), составляющие по данным табл. 8.13:

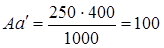и

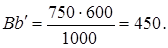
При отсутствии связи на первой диагонали таблицы в сумме было бы 100 + 450 = 550 единиц совокупности, а на самом деле их 170 + 520 = 690. Избыток, образовавшийся ввиду прямой связи между ответами, составил 690—550 = 140.

Предельно возможный избыток был бы в том случае, если бы не было гетерогенных сочетаний, т. е. Аb и Bа. Он составляет 140+80 + 230 = 450. Сам же показатель тесноты связи - отношение фактического излишка к предельному: 140 : 450 =0,311. Как видим, этот показатель близок к коэффициенту ассоциации, но обладает чрезвычайно логичной и ясной интерпретацией: связь составляет 0,311 или 31,1%, от предельно возможной функциональной. Этот показатель - аналог не коэффициента корреляции, а коэффициента детерминации. Поэтому правомерно обозначить его как R² или η² . Он имеет вид:

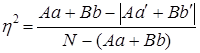, (8.49)

где

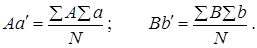
Подставляя эти выражения в (8.49), получим:

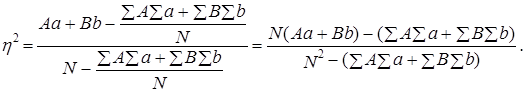(8.50)*

При наличии не двух, а более возможных значений каждого из взаимосвязанных признаков также разработаны разные методы измерения тесноты связи.

Рассмотрим некоторые из этих мер на примере изучения влияния религиозной принадлежности на формирование супружеских пар. Воспользуемся данными ФРГ, где такой учет ведется постоянно. Статистический ежегодник Федеративной Республики Германии приводит распределение живорожденных младенцев по религиозной принадлежности отца и матери. При этом выделены 5 групп по религиозной принадлежности граждан: евангелическая (в России их чаще именуют протестантами); 2) римско-католическая; 3) прочие христиане (включая и православных); 4) других религий; 5) неверующие или не указавшие религиозную принадлежность (табл. 8.16).

Таблица 8.16