Распределение футбольных матчей высшей лиги России по числу забитых за матч обеими командами мячей в 1996 г.

Среднее число мячей, забитых за одну игру, должно представлять собой результат равномерного распределения общего числа забитых мячей по всем 306 матчам розыгрыша первенства. Общее число забитых мячей, согласно исходной информации табл. 5.1, можно получить как сумму произведений значений признака в каждой группе х_i, на число игр с таким количеством забитых мячей f_i (частоты). Получим формулу (5.2)

,

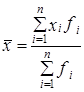где п — число групп.

Такую форму средней арифметической величины называют взвешенной арифметической средней в отличие от простой средней, рассчитанной по формуле (5.1). В качестве весов выступают здесь числа единиц совокупности в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины. «Важнее», весомее число забитых мячей, которое встречалось чаще: 1, 2, 3 мяча, а такие значения, как 7 или 9 забитых мячей, как бы ни радовались таким результативным матчам болельщики, при расчете средней не играют большой роли: их «вес» мал.

Имеем: х̅ = 802 : 306 = 2,62 мяча за игру.

Как видим, средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения (дискретный признак). Ничего «предосудительного» для метода средних в этом не заключено; из сущности средней не вытекает, что она обязана быть реальным значением признака, которое могло бы встретиться у какой-либо единицы совокупности.