Сборочная размерная цепь с линейными звеньями

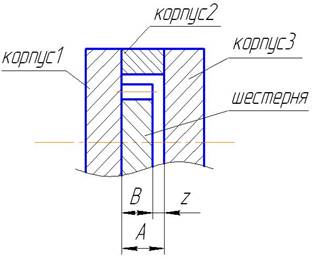Обычно имеет место при определение погрешности зазора, натяга, длины и т.д.. Рассмотрим сборку шестереночного насоса:

Размеры тип А будут увеличивающимися; размеры типа В – уменьшающими, т.к. при увеличении первого размера замыкающие звено увеличивается, а при увеличение второго типа замыкающие звено уменьшается.

В общем случае когда звено состоит из n звеньев, из которых m являются увеличивающих, и от m+1 до n-1 – уменьшающих звеньев

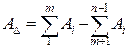
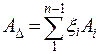–основное уравнение номинальных размеров линейных цепей.

Коэффициент 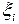называется передаточным отношением или коэффициент влияния. Он характеризует степень влияния составляющего звена на замыкающий размер. Для рассматривания размерных цепей с n звеньями 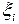= +1 для увеличивающих размеров и 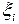= -1 для уменьшающих размеров.

Для расчета точности, т.е. величины предельных отклонений замыкающего размера используют два метода расчета а именно:

1) метод максимум-минимум;

2) теоретико-вероятностный метод.

При расчете по методу максимума-минимума предполагается, что составляющие звенья размерной цепи (размеры детали которые входят в цепь) выполнены с наименее выгодным предельными отклонениями, т.е. таким образом что величина допуска замыкающего звена уменьшается, т.е. когда увеличивающие размеры выполнены по минимуму а уменьшающие размеры выполнены по максимуму, тогда наибольшее значение

А_Δmax = (А_1max + A_2max) – (A_5min + A_4min + A_3min + A_6min)

А_Δmin = (А_1min + A_2min) – (A_5max + A_4max + A_3max+ A_6max)

В общем случае m увеличивающих от m+1 до n-1 уменьшающих

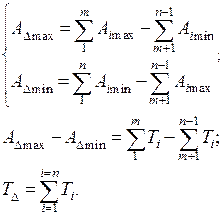
Допуск замыкающего звена равен арифметической сумме допусков составляющих звеньев. При расчете по методу максимум-минимум берется самый худший случай, когда детали изготовлены с предельными отклонениями размеров. Из этого следует, что результаты расчетов многократно завышены, поэтому этот метод применяется для ориентировочных расчетов. Или для окончательных расчетов, но только в случае если сборка идет по методу полной взаимозаменяемости.

Более верным и более соответствующим условиям является метод расчета с использованием теории вероятности. В отличие от метода расчета по максимуму-минимуму в данном случае оперируют не номинальными значениями размеров, а средними размерами и рассеивания их отклонений относительно среднего значения.

Из теории вероятности известно, что если на результат какого либо процесса влияют большое число однородных по величине факторов, то распределение результатов процесса будет подчиняться закону Гаусса, т.е. закону распределения случайных величин, или мало от него отличаться. В авиадвигателестроении производство большинства деталей ведется на настроенных станках, следовательно получаемые размеры этих деталей в партии подчиняются нормальному закону распределения. Это нашло свое отражение в том, что расчетные уравнения прямо или косвенно включают параметры математического закона Гаусса. Отклонение от него или отсутствие данных о законах учитываются с помощью введения соответствующих коэффициентов

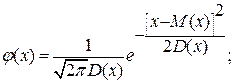
M(x) – математическое ожидание или среднее значение центра группирования отклонения случайной величины от номинального значения;

D(x) – дисперсия – характеризует меру рассеивания отклонений

СКО σ = 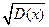- среднеквадратичное отклонение от математического ожидания.

Для расчета цепей по данному методу используют две теоремы из теории вероятности, которые относятся к закону накопления случайной величины.

1) Среднее значение суммы или разности случайной величины равно сумме или разности средних значений.

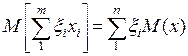
2) Дисперсия суммы или разности равна сумме дисперсии или разности случайных величин

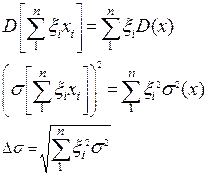
При сборке рассеивание размеров замыкающего звена будет следовать закону Гаусса и не менее чем для 99,73% сборочных единиц замыкающее звено будет находиться в пределах ограниченных допуском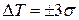

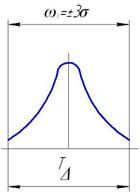Если теперь СКО поля рассеяния заменить полями допусков, то 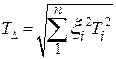- основная сумма составляющих погрешностей по теоретико-вероятностному методу если составные звенья подчиняются закону нормального распределения. В общем случае когда поля рассеяния не подчиняются закону нормального распределения, то допуск замыкающего звена рассчитывается по следующей формуле

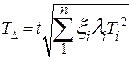
t – коэффициент риска характеризующий процент выхода расчета отклонений за пределы допуска.