Математическая модель системы изменения вылета портальных кранов в виде механизмов с жесткими звеньями

Перед тем как перейти к расчету механизмов изменения вылета, необходимо разработать математическую модель системы изменения вылета портального крана при работе механизма изменения вылета.

Введем в рассмотрение КПФ первого порядка

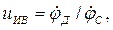
где 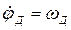– угловая частота вращения ротора двигателя МИВ. Разобьем u_ив на две составляющие:

u_ив = u_М u_Р, (1.93)

где 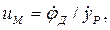; ; 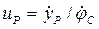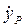— линейная скорость движения тягового звена (рейки, винта, полиспаста). Положительное направление y_P показано на рис. 1.37.

u_М определяется в зависимости от типа МИВ. Для реечного МИВ

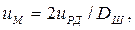
где u_РД — передаточное число редуктора МИВ; 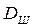— диаметр кремальной шестерни.

Для винтового МИВ угловая частота вращения гайки (винта) 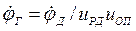, где u_ОП — передаточное отношение открытой передачи. Поступательная скорость винта

,

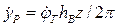где h_В — шаг резьбы, z — число заходов. Тогда в соответствии с (1.94) u_Мбудет определяться по формуле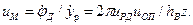

Для полиспастного МИВ скорость каната стрелового полиспаста 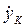, навиваемого на барабан лебедки, 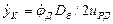, где D_б — диаметр барабана лебедки по средней линии каната. И u_м = 2 u_стр u_рд / D_б, где u_стр — кратность стрелового полиспаста.

При постоянной частоте вращения ротора двигателя скорость горизонтального перемещения груза 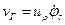переменна по вылету (рис. 1.60).

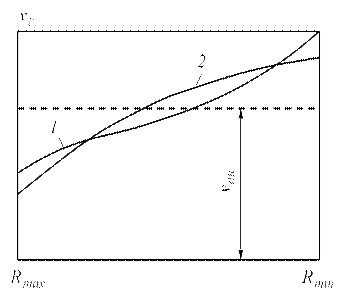Рис. 1.60. Графики изменения скорости горизонтального перемещения груза при установившемся движении привода МИВ: 1 — для шарнирно-сочлененной стрелы при реечном или винтовом МИВ; 2 — для прямой стрелы при полиспастном или секторном МИВ

Постоянная скорость тягового звена 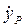находится исходя из средней скорости v_ив горизонтального перемещения груза. Время t_ив, за которое вылет стрелы изменяется от R_max до R_min: t_ив = (R_max – R_min) / v_ив. Тогда скорость тягового звена(см. рис. 1.57)

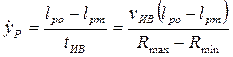. (1.95)

Для нахождения кинематической передаточной функции первого порядка u_Р рассмотрим схему на рис.1. 41. Длина тягового звена

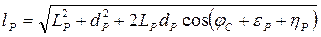(1.96)

Изменение длины l_р тягового элемента l_ро — начальная длина, y_р — линейное перемещение. Продифференцировав по времени это соотношение с учетом (1.96), найдем выражение для u_Р в соответствии с (1.94):

u_Р = L_Р d_Р sin(j_c +e_Р + h_Р)/l_Р, (1.97)

где l_р определяется по (1.96).

На рис. 1.61 представлены в качестве примера графики КПФ первого порядка для системы изменения вылета портального крана АО «Подъемтрансмаш» КПП 10(12,5) – 30, рассчитанные с помощью приведенных выше формул. Большинство из них носит сугубо нелинейный характер.

Для разработки математической модели системы изменения вылета портальных кранов в виде механизма с жесткими звеньями рассмотрим схему на рис. 1.41. Будем считать, что движение элементов СИВ и груза происходит в неподвижной системе координат y_к 0_к z_к, ось 0_к z_к которой направлена по оси вращения крана. Груз на канатах моделируется в виде математического маятника.

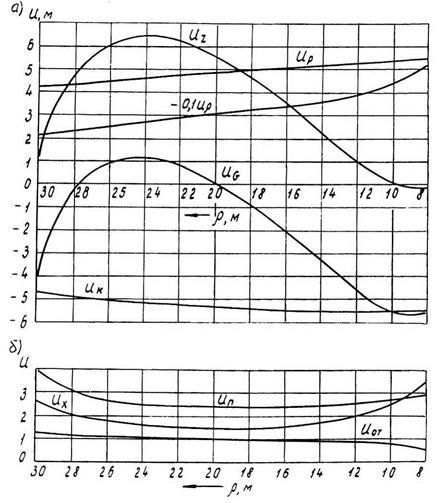Рис. 1.61. Кинематические передаточные функции первого порядка системы изменения вылета портального крана КПП 10(12,5) –30 АО «Подъемтрансмаш»

В качестве независимых обобщенных координат примем угол j_с наклона стрелы и отклонение y_г груза от положения равновесия. Для вывода уравнений движения воспользуемся уравнениями Лагранжа второго рода.

Кинетическая энергия Т системы складывается из кинетических энергий:

стрелы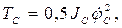

хобота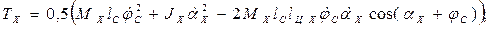

оттяжки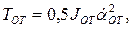

противовеса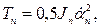

элементов механизма изменения вылета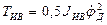

груза .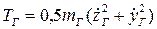

В приведенных соотношениях J_c, J_x, J_от, J_п — моменты инерции стрелы, хобота, оттяжки и противовеса соответственно относительно точек 0₁, 0_с, 0₃, 0₄ (см. рис. 1.41), М_х — масса хобота, J_ИВ — момент инерции вращающихся элементов МИВ: J_и.в = 1,2 (J_р + J_м), где J_р и J_м — соответственно моменты инерции ротора двигателя и муфт с тормозными шкивами.

Координаты y_Кг и z_Кг центра масс груза в системе y_к 0_к z_к найдутся в соответствии со схемой на рис. 1.37 в виде

y_Кг = r + y_г, 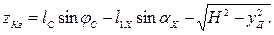(1.98)

Используя выражения для кинематических передаточных функций, для кинетической энергии можно записать выражение вида

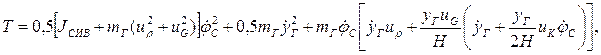
где приведенный к координате j_с момент инерции элементов СИВ определяется по формуле

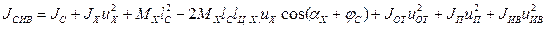. (1.99)

Потенциальная энергия П сил тяжести элементов СИВ складывается из потенциальной энергии стрелового устройства П_с (1.68), уравновешивающего устройства П_п (1.69) или (1.81) и груза П_г = G_г z_Кг, где z_Кг определяется по (1.98).

Непотенциальные обобщенные силы, действующие на СИВ с грузом – М_ст, М_в, Р_в, М_ИВ; М_ст — статический момент сопротивления движению стрелы, связанный с наличием сил трения в шарнирах соединений элементов СИВ и сил трения при перекатывании грузовых канатов; М_в и Р_в — соответственно момент сил сопротивления движению стрелы, связанный с ветровой нагрузкой на конструкцию стреловой системы (см. рис. 1.63), и сила ветра, действующая на груз в плоскости стреловой системы.

Эти величины определяются по рекомендациям, имеющимся в литературе [12, 14]. М_ив — момент двигателя (тормоза), приведенный к координате j_с. Для двигательного режима М_ив = М_д u_ивh_о, для режима торможения М_ив = –М_т u_ив/h_о, где М_д и М_т — соответственно моменты двигателя и тормоза на валу двигателя, h_о — КПД механизма изменения вылета.

Используя уравнения Лагранжа второго рода, получим систему дифференциальных уравнений, описывающую движение СИВ крана с грузом:

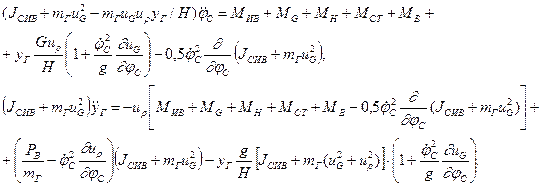(1.100)

Полученная система уравнений (1.100) не изменяется при различных исполнениях стреловой системы, уравновешивающего устройства и механизма изменения вылета. Так, например, схему уравновешивающего устройства характеризуют лишь значения М_пр и u_п. Это обстоятельство позволяет использовать одну систему уравнений для сравнения элементов СИВ, выполненных по различным схемам.

Система уравнений (1.100) позволяет эффективно исследовать аварийные режимы работы СИВ — обрыв тягового звена или отказ тормозов. В этом случае стреловая система начинает движение к положению равновесия и проходит его за счет сил инерции; возможны достижение крайних положений и удары о концевые упоры.

Для крана без груза крайнее смещение стреловой системы (СС) при повороте стрелы в вертикальной плоскости (наклоне стрелы) на угол j_ск может быть найдено следующим образом. Уравнение, описывающее движение СИВ крана без груза в аварийном режиме, можно при некоторых упрощениях записать в виде

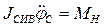. (1.101)

В случае обрыва тягового звена член 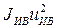в выражении (1.99) полагается равным нулю. Так как 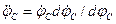, то разделяя переменные, получим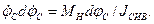

Полагая, что обрыв тягового звена или отказ тормозов происходит при нулевой скорости 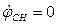и угле j_сн, получим первый интеграл уравнения (1.101) в виде

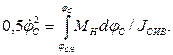(1.102)

Величина угла j_ск, которого достигнет стреловая система крана в аварийном режиме, определится из (1.102) при условии 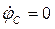по формуле:

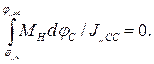
Полученное значение j_ск будет несколько выше действительного, так как в этом случае не учитываются силы трения, действующие в системе.

На рис. 1.62 представлены расчитанные на ЭВМ фазовые траектории конца хобота портального крана КПП 10(12,5) – 30 без груза.

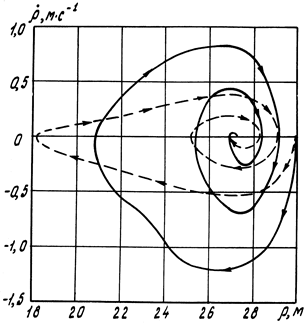Рис. 1.62. Фазовые траектории концевых блоков хобота крана КПП 10(12,5) – 30 без груза при обрыве рейки (пунктирная линия) и отказе тормозов (сплошная линия)

При отказе тормоза приведенный момент инерции СИВ J_сив и момент сил трения выше, чем при обрыве рейки.