На горизонтальные и вертикальные расстояния
Для обработки результатов геодезических измерений и для получения топографических материалов точки земной поверхности проецируют отвесными линиями на поверхность более простую, чем земная.Такой поверхностью могут быть поверхности референц-эллипсоида, шара или плоскости. В геодезии используют проецирование точек линиями, перпендикулярными к поверхности относимости. Такое проектирование называют ортогональным. На рисунке 3.1 показано ортогональное проектирование контура ABCDE земной поверхности на поверхность референц-эллипсоида (см. рисунок 3.1, а) и плоскость (см. рисунок 3.1, б).
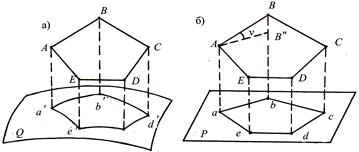 |
Рисунок 3.1 – Ортогональное проектирование
Как видно из рисунка 3.1, при ортогональном проектировании на референц-эллипсоид проекцией многоугольника ABCDE будет сферический многоугольник a'b'c'd'e', а при ортогональном проектировании многоугольника ABCDE на плоскость его проекцией будет плоский многоугольник abcde, который называют горизонтальной проекцией участка местности. Стороны плоского многоугольника ab, bc и т. д. являются горизонтальными проложениями соответствующих сторон пространственного многоугольника АВ, ВС и т. д. Как видно из рисунка 3.1, б горизонтальное проложение линии всегда меньше наклонной длины линии на местности.
d = D cosν,
где ν – угол наклона линии местности к плоскости Р.
Углы abc, bcd и т. д. – являются горизонтальными проекциями соответствующих углов на местности и называются горизонтальными углами. Изучение формы и размеров сферической проекции фигуры местности является более сложным, чем изучение плоской проекции, кроме этого сферическую проекцию нельзя изобразить в подобном виде на плоскости из-за влияния кривизны Земли. Поэтому возникает вопрос, при каких расстояниях на земной поверхности кривизну уровенной поверхности Земли можно не учитывать или при каких расстояниях можно сферическую фигуру местности принимать за плоскую. Рассмотрим этот вопрос более подробно. Примем
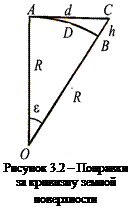 фигуру Земли за шар радиусом R (рисунок 3.2). О – центр земного шара. Через точку А проведена горизонтальная плоскость, перпендикулярная к радиусу ОА. Разность между длиной касательной АС = d и длиной дуги АВ = D будет составлять погрешность в горизонтальном расстоянии при замене сферической поверхности плоскостью. Величина этой погрешности будет Δd = d – D.
фигуру Земли за шар радиусом R (рисунок 3.2). О – центр земного шара. Через точку А проведена горизонтальная плоскость, перпендикулярная к радиусу ОА. Разность между длиной касательной АС = d и длиной дуги АВ = D будет составлять погрешность в горизонтальном расстоянии при замене сферической поверхности плоскостью. Величина этой погрешности будет Δd = d – D.
Из треугольника ОАС находим d = R tgε. Длина дуги окружности D = Rε, где ε – центральный угол, выраженный в радианной мере. Тогда
Δd = d – D = R (tgε – ε). (3.1)
Из математики известно, что tgε можно разложить в ряд, ограничившись первыми двумя слагаемыми ряда:
tgε = ε + ε3/3 + …,
откуда, учитывая (3.1), получим
Δd = R(ε + ε3/3) – ε = Rε3/3.
Поскольку из выражения D = Rε; ε = D/R, то
Δd = RD3/3R3 = D3/3R2. (3.2)
При R ≈ 6000 км и D = 10 км получим
Δd/D = D2/(3R2) = 102/(3 · 36 · 104) ≈ 1/106 = 1/1000000.
Такой погрешностью характеризуются наиболее точные измерения линий в геодезии. Следовательно, участки земной поверхности размером 20×20 км можно считать плоскими, и в отношении расстояний, меньших 20 км, сферическую проекцию участков местности можно принимать за плоскую.
В отношении углов сферической проекции многоугольника имеется формула сферического избытка (q), который показывает, насколько сумма углов в сферическом многоугольнике больше чем в плоском:
q = ρP/R2, (3.3)
где ρ – величина радиана (ρ = 57о17'45'' = 3438' = 206265'');
Р – площадь фигуры;
R – радиус земного шара.
Для Р = 10×10 км = 100 км2 q = 0,51'', для Р = 20×20 км = 400 км2 q = 2,03''.
Таким образом, при угловых измерениях с погрешностями более 2'' для участков местности 20×20 км величина сферического избытка не превышает требуемой точности и влияние сферичности Земли можно не учитывать.
Из приведенных расчетов не следует делать вывод, что для линий, меньших 20 км можно не принимать во внимание влияние кривизны Земли при любых геодезических измерениях. Так, например, величина погрешности в вертикальном расстоянии, т. е. в высоте точки В, выразится отрезком ВС = h (cм. рисунок 3.2):
h = ОС – ОВ.
Из прямоугольного треугольника ОАС определим
d2 = (R + h)2 – R2 = R2 + 2Rh + h2 – R2 ,
откуда
h = d 2/(2R + h). (3.4)
Поскольку величина h мала по сравнению с радиусом Земли, то в знаменателе формулы (3.4) ею можно пренебречь, и тогда получим:
h = d 2/2R. (3.5)
Придавая d в формуле (3.5) различные значения и приняв R = 6000 км, получим: для d = 100 м – h = 1 мм, для d = 300 м – h = 8 мм, для d = 2000 м – h = 33,4 мм.
При строительстве инженерных сооружений погрешности высотных измерений не должны превышать 1–2 мм, поэтому влияние кривизны Земли на определение высоты должно учитываться уже для расстояний более 100 м.
3.2 Топографические материалы: план, карта, профиль
К топографическим материалам относятся: план, карта и профиль. Топографическим планом называют уменьшенное и подобное изображение на бумаге горизонтальных проекций участков местности. Как было показано выше, подобное изображение получают при ортогональном проецировании участков земной поверхности, не превышающих 20×20 км на горизонтальную плоскость. В уменьшенном виде на бумаге такое изображение называют планом местности.
Изображение больших по размерам участков земной поверхности (более чем 20×20 км) на плоскость нельзя получить без искажений, т. е. с сохранением полного подобия. Такие участки ортогонально проецируют на поверхность референц-эллипсоида, а затем с поверхности эллипсоида по определенным математическим законам, называемым картографическими проекциями, переносят на плоскость. Полученное таким образом уменьшенное на бумаге изображение значительных участков земной поверхности (более 20 км) с учетом кривизны Земли называют картой. Карта, составленная в проекции Гаусса-Крюгера, называется топографической картой.
На топографических планах и картах показывают ситуацию и рельеф местности. С и т у а ц и е й называют совокупность контуров и предметов местности. Ситуация является плановой частью местности (лес, луг, пашня, гидрография, здания, дороги, линии водопровода, гидротехнические объекты и т. д.). Ее изображают на планах и картах условными топографическими знаками.
Р е л ь е ф о м называется совокупность неровностей земной поверхности. Рельеф – высотная часть местности. Она изображается на картах и планах в виде горизонталей – плавных кривых линий, проходящих через точки с равными высотами (отметками).
Основные требования, предъявляемые к топографическим картам и планам, являются точность и наглядность.
Под т о ч н о с т ь ю понимают соответствие местоположения, очертаний и размеров объектов на планах и картах действительности. Н а г л я д - н о с т ь планов характеризуется зрительным восприятием образа земной поверхности, ее характерных черт и особенностей.
Основными характеристиками точности планов и карт является масштаб, а наглядности – условные топографические знаки и цветовое оформление. Кроме планов и карт к топографическим материалам относятся профили местности, представляющие собой уменьшенное на бумаге изображение вертикального разреза поверхности Земли по заданному направлению. Профили местности являются топографической основой при составлении проектной документации, необходимой при строительстве железных и автомобильных дорог, линий водоснабжения и канализации и других коммуникаций.
Масштабы планов и карт. Точность масштаба
При изображении участков земной поверхности на плане или карте размеры этих участков уменьшают в известное число раз. Степень уменьшения линий на плане по отношению к их горизонтальным проложениям (проекциям) на местности называется масштабом.
Масштабы могут быть численные, линейные и поперечные. Ч и с л е н -н ы м масштабом называется выражение в виде дроби числителем, которой является единица, а знаменателем – число, показывающее, во сколько раз линии на плане уменьшены по отношению к их горизонтальным проекциям на местности. Например, выражение 1: 2000 показывает, что в 1 см на плане содержится 2000 см (20 метров) местности. Зная численный масштаб плана, можно определить по длине линии местности соответствующую длину линии на плане и наоборот. Например, если длина линии на плане равна 3,23 см, а масштаб плана – 1:2000 то соответствующая линия на местности будет
d = 3,23 см × 2000 = 6460 см = 64,60 м.
Или, если длина линии на местности равна 200 м, то на плане масштаба 1:5000 длина соответствующего отрезка будет
l = 200 м : 5000 = 0,04 м = 4 см.
Для того чтобы не производить таких вычислений, обычно пользуются специальными графическими масштабами: линейным и поперечным. Для построения л и н е й н о г о масштаба берут прямую линию и на ней откладывают равные отрезки, называемые основанием масштаба (рисунок 3.3).
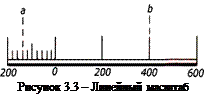 Левый крайний отрезок делят на 10 равных частей. Рассчитав по численному масштабу длину линии местности, соответствующую основанию масштаба, подписывают деления линейного масштаба. На рисунке 3.3 основание масштаба взято 2 см. При численном масштабе 1:10000 2 см на плане соответствует 200 м на местности. Следовательно, на линейном масштабе отрезки справа от нуля будут соответствовать 200 м на местности, а влево по 20 м. Для того чтобы отложить на плане линию, равную 540 м на местности нужно с помощью циркуля-измерителя отложить отрезок ab (см. рисунок 3.3). Как видно, отрезки меньше 2 мм в данном масштабе оцениваются на глаз. Для того чтобы расстояние по масштабу можно было откладывать более точно, строят п о п е -р е ч н ы й масштаб. На прямой AF (рисунок 3.4) несколько раз откладывают основание масштаба (обычно 2 см) и из полученных точек восстанавливают к ней перпендикуляры. Один из перпендикуляров делят на 10 частей и через точки деления проводят линии, параллельные AF. Левый отрезок AO делят на 10 частей. Верхнее левое основание делят также на 10 равных частей. Точки верхнего и нижнего левых оснований соединяют наклонными линиями так, как показано на рисунке 3.4. Из рисунка 3.4 видно, что наименьшее деление поперечного масштаба
Левый крайний отрезок делят на 10 равных частей. Рассчитав по численному масштабу длину линии местности, соответствующую основанию масштаба, подписывают деления линейного масштаба. На рисунке 3.3 основание масштаба взято 2 см. При численном масштабе 1:10000 2 см на плане соответствует 200 м на местности. Следовательно, на линейном масштабе отрезки справа от нуля будут соответствовать 200 м на местности, а влево по 20 м. Для того чтобы отложить на плане линию, равную 540 м на местности нужно с помощью циркуля-измерителя отложить отрезок ab (см. рисунок 3.3). Как видно, отрезки меньше 2 мм в данном масштабе оцениваются на глаз. Для того чтобы расстояние по масштабу можно было откладывать более точно, строят п о п е -р е ч н ы й масштаб. На прямой AF (рисунок 3.4) несколько раз откладывают основание масштаба (обычно 2 см) и из полученных точек восстанавливают к ней перпендикуляры. Один из перпендикуляров делят на 10 частей и через точки деления проводят линии, параллельные AF. Левый отрезок AO делят на 10 частей. Верхнее левое основание делят также на 10 равных частей. Точки верхнего и нижнего левых оснований соединяют наклонными линиями так, как показано на рисунке 3.4. Из рисунка 3.4 видно, что наименьшее деление поперечного масштаба
t = AO / 100 = 2 см / 100 = 0,2 мм.
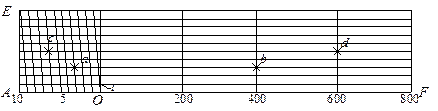
Рисунок 3.4 – Поперечный масштаб
На рисунке 3.4 роспись поперечного масштаба сделана для численного масштаба 1:10000 при основании масштаба 2 см. Расстояния 466 и 730 м на поперечном масштабе отмечены точками ab и cd, в которые нужно установить ножки циркуля-измерителя. Невооруженным глазом отрезки на плане, меньше 0,1 мм становятся неразличимыми и практически являются точкой. Поэтому расстояние на местности, которое соответствует 0,1 мм на плане, принято называть точностью масштаба плана. В соответствии с этим точность стандартных численных масштабов топографических планов и карт приведена в таблице 3.1. Расчет выполнялся по формуле
t = 0,1 мм · М,
где M – знаменатель масштаба.
Таблица 3.1 – Точность масштабов топографических планов и карт
| Характеристика планов и карт | Численный масштаб | Точность масштаба в метрах | Расстояние на местности в метрах, соответствующее 1 см плана (карты) | |
| Планы | крупномасштабные | 1:200 1:500 | 0,02 0,05 | |
| среднемасштабные | 1:1000 1:2000 | 0,1 0,2 | ||
| мелкомасштабные | 1:5000 | 0,5 | ||
| Карты | крупномасштабные | 1:10000 1:25000 1:50000 | 1,0 2,5 5,0 | |
| среднемасштабные | 1:100000 1:200000 | 10,0 20,0 | ||
| мелкомасштабные | 1:500000 1:100000 | 50,0 100,0 |
Из приведенных данных видно, что чем меньше величина знаменателя численного масштаба, тем крупнее масштаб плана или карты и тем выше его точность. Точность масштаба позволяет определить, какие предметы местности могут быть изображены на плане или карте в виде подобной фигуры, а какие за малостью своих размеров обратятся на плане в точку. Например, здание длиной и шириной 5 м в масштабе 1:50000 изобразится на плане в виде одной точки.
Важное практическое значение имеет и обратный вопрос: в каком масштабе нужно составлять план, чтобы определенные предметы местности были изображены на этом плане с сохранением подобия? На этот вопрос можно ответить, если проанализировать точность масштаба согласно таблице 3.1. При этом нужно иметь в виду, что наименьший отрезок на плане, который мы различаем как отрезок, а не как точку, равен 0,2 мм. Поэтому, например, для масштаба 1:2000 мы можем различить предметы местности, которые не менее 0,2 мм на плане, что соответствует 0,4 м на местности.
Дата добавления: 2015-01-19; просмотров: 2456;
