Прямая и обратная геодезические задачи. Прямая геодезическая задача используется для определения координат точек на местности

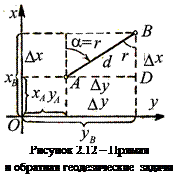Прямая геодезическая задача используется для определения координат точек на местности. Пусть известны координаты начальной точки (X_A, Y_A), дирекционный угол линии α_АВ и расстояние между точками d_АВ. Тогда по этим данным можно определить координаты второй точки В (рисунок 2.12). Согласно рисунку 2.12 имеем:

X_B – X_A = ΔX; Y_B – Y_A = ΔY.

Разности ΔX и ΔY координат точек называют п р и р а щ е н и я м и к о о р д и н а т. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Из треугольника ABD следует, что

ΔX = d сos α_AB ; ΔY = d sin α_AB. (2.9)

Приращения координат могут быть положительными и отрицательными, в зависимости от направления линий. Поскольку ось XX в геодезии совпадает с направлением меридиана, то можно составить таблицу для определения знака приращения координат (таблица 2.4).

Таблица 2.4 – Знаки приращений координат

Номер четверти	Дирекционный угол, град	Знаки приращения координат
DX	DY
I II III IV	0–90 90–180 180–270 270–360	+ – – +	+ + – –

Определив приращения координат по формулам (2.9), находят координаты второй точки В:

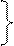Х_В = Х_А + ΔХ = Х_А + d cosα_АВ;

(2.10)

Y_B = Y_A + ΔY = Y_A + d sinα_AB.

Из формулы (2.10) следует правило для вычисления координат точки. Координаты последующей точки равны координатам предыдущей точки плюс соответствующее приращение координат. Приращения координат можно вычислять на микрокалькуляторе или по специальным таблицам.

Обратная геодезическая задача. В обратной геодезической задаче требуется определить длину линии АВ = d и ее направление (дирекционный угол α_АВ) по заданным координатам точек А (X_A, Y_A) и В (X_B, Y_B) (см. рисунок 2.12).

Согласно формулам (2.9) можно написать:

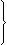d cosα_AB = ΔX = X_B – X_A;

(2.11)

d sinα_AB = ΔY = Y_B – Y_A.

Разделив левые и правые части этих равенств, получим

tg α_AB = (Y_B – Y_A) / (X_B – X_A) = ΔY / ΔX. (2.12)

Согласно (2.11) найдем:

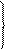d = (X_B – X_A) / cosα_AB = ΔX / cosα_AB;

(2.13)

d = (Y_B – Y_A) / sinα_AB = ΔY / sinα_AB.

Из треугольника АВД (см. рисунок 2.12) получим контрольную формулу для d:

d = √ ΔX² + ΔY² = √ (X_B – X_A)² + (Y_B – Y_A)². (2.14)

При определении α по формуле (2.12) согласно таблице 2.4 по знакам ΔX и ΔY определяют четверть, в которой находится угол, затем – румб линии АВ r = arctg ΔY/ΔX и по номеру четверти, используя формулы таблицы 2.3, – дирекционный угол α_АВ.

ТОПОГРАФИЧЕСКИЕ ПЛАНЫ И КАРТЫ

<4 5 678 9 10 >

Дата добавления: 2015-01-19; просмотров: 1813;