Числа заполнения

• Приближение: электронный газ в кристалле считают идеальным газом.

• Состояние системы задается с помощью чисел заполнения.

• Числа заполнения N указывают степень заполнения квантового состояния.

Квантовое состояние зависит от спина частиц.

Все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса.

Частицы с полуцелым спином (например,

электроны, протоны, нейтроны) подчиняются статистике Ферми — Дирака; эти частицы называются фермионами.

Частицы с нулевым или целочисленным спином (фотоны) подчиняются статистике Бозе — Эйнштейна; эти частицы называются бозонами.

Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин —полуцелый), а из четного — бозонами (суммарный спин целый).

• Для систем частиц, образованных бозонами числа заполнения могут принимать любые целые значения: 0, 1, 2, ...

• Для систем частиц, образованных фермионами числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых.

• Сумма всех чисел заполнения должна быть равна числу частиц системы

Идеальный газ из бозонов описывается квантовой статистикой Бозе — Эйнштейна

Ni) — среднее число бозонов в квантовомсостоянии с энергией Ei,

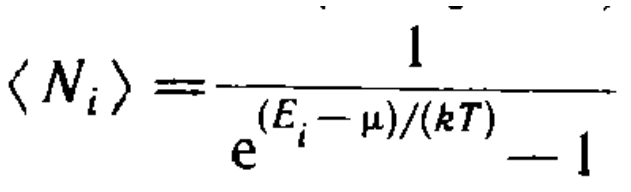
k — постоянная Больцмана,

Т — термодинамическая температура,

μ — химический потенциал;

( μ не зависит от энергии, а определяется только температурой и плотностью числа частиц. )

Идеальный газ из фермионов описывается квантовой статистикой Ферми — Дирака:

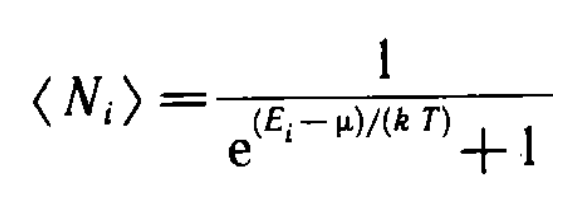
• Если 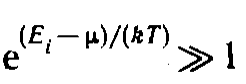, то распределения

Бозе — Эйнштейна и Ферми — Дирака переходят в классическое распределение Максвелла — Больцмана: где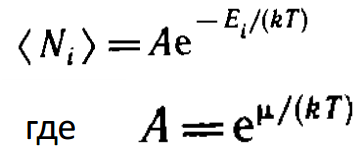

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.