Построение статистических рядов
Выборка, полученная при проведении экспериментального исследования, представляет собой неупорядоченный набор чисел, записанных в той последовательности, в которой производились измерения. Обычно выборка оформляется в виде таблицы, в первой строке (или столбце) которой стоит номер опыта i, а во второй (втором) - зафиксированное значение случайной величины признака. В таком виде выборка представляет собой первичную форму записи статистического материала, который может быть обработан различными способами. В качестве примера рассмотрим результаты, показанные на легкоатлетических соревнованиях толкателями ядра и приведенные в таблице 1. В первой строке этой таблицы записаны номера измерений, а во второй - их численные значения в метрах.
Таблица 1
Результаты соревнований в толкании ядра
| № | ||||||||||
| xi | 16,36 | 14,91 | 15,31 | 14,26 | 14,77 | 13,88 | 14,97 | 14,01 | 14,07 | 14,48 |
| № | ||||||||||
| xi | 14,44 | 14,81 | 13,81 | 15,15 | 15,23 | 15,69 | 14,29 | 14,15 | 14,57 | 13,92 |
| № | |||||||||
| xi | 13,62 | 14,92 | 15,73 | 13,22 | 14,65 | 14,8 | 13,04 | 15,1 | 13,3 |
Как видно из таблицы 1, простая статистическая совокупность перестает быть удобной формой представления статистического материала даже при относительно небольшом объеме выборки: она является достаточно громоздкой и мало наглядной. Проанализировать полученные экспериментальные данные и тем более сделать какие-либо выводы на их основе весьма затруднительно. Исходя из этого, полученный статистический материал должен быть обработан для проведения дальнейшего исследования. Простейшим способом обработки выборки является ранжирование. Ранжированием называют расстановку вариант в порядке возрастания или убывания их значений. Ниже в таблице 2 приведена ранжированная выборка, элементы которой расположены в порядке возрастания.
Таблица 2
Ранжированные результаты соревнований в толкании ядра
| № | ||||||||||
| xi | 13,04 | 13,22 | 13,3 | 13,62 | 13,81 | 13,88 | 13,92 | 14,01 | 14,07 | 14,15 |
| № | ||||||||||
| xi | 14,26 | 14,29 | 14,44 | 14,48 | 14,57 | 14,65 | 14,77 | 14,8 | 14,81 | 14,91 |
| № | |||||||||
| xi | 14,92 | 14,97 | 15,1 | 15,15 | 15,23 | 15,31 | 15,69 | 15,73 | 16,36 |
Но и в таком виде полученные экспериментальные данные плохо обозримы и мало пригодны для непосредственного анализа. Именно поэтому для придания статистическому материалу большей компактности и наглядности он должен быть подвергнут дальнейшей обработке – строится так называемый статистический ряд. Построение статистического ряда начинается с группировки.
Группировкой называется процесс упорядочения и систематизации данных, полученных в ходе проведения эксперимента, направленный на извлечение содержащейся в них информации. В процессе группировки осуществляется распределение вариант выборки по группам или интервалам группировки, каждый из которых содержит некоторый диапазон значений изучаемого признака. Процесс группировки начинается с разбиения всего диапазона варьирования признака на интервалы группировки.
Для каждой конкретной цели статистического исследования, объема рассматриваемой выборки и степени варьирования признака в ней существует оптимальное значение числа интервалов и ширины каждого из них. Ориентировочное значение оптимального числа интервалов k может быть определено, исходя из объема выборки п либо с помощью данных, приведенных в таблице 3., либо с помощью формулы Стэрджесса:
k = 1 + 3,322 lgn.
Таблица 3
Определение числа интервалов группировки
| Объем выборки n | 10-30 | 30-60 | 60-100 | 100-300 | 300-400 |
| Число интервалов k | 4-5 | 5-6 |
Получаемое по формуле значение k почти всегда оказывается дробной величиной, которую необходимо округлить до целого числа, поскольку количество интервалов не может быть дробным. Практика показывает, что, как правило, лучше округлять в меньшую сторону, ибо формула дает хорошие результаты при больших значениях n, а при малых - несколько завышенные.
Рассмотрим группировку вариант выборки на конкретном примере. Для этого обратимся к примеру с толкателями ядра (см. таблицы 1, 2). Определение числа интервалов группировки будем производить на основе данных, приведенных в таблице 3. При объеме выборки n=29 число интервалов целесообразно выбрать равным k =5 (формула Стэрджесса дает значение k =5,9).
Условимся использовать в рассматриваемом примере интервалы равной ширины. В этом случае после того, как число интервалов группировки определено, следует вычислить ширину каждого из них с помощью соотношения:
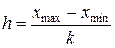 .
.
Здесь h - ширина интервалов, а хmax и хmin - соответственно максимальное и минимальное значение признака в выборке. Величины хmax и хmin определяются непосредственно по таблице исходных данных (см. таблицу 2). В рассматриваемом случае:
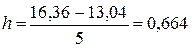 (м).
(м).
Здесь необходимо остановиться на точности определения ширины интервала. Возможны две ситуации: точность вычисленного значения h совпадает с точностью проведения эксперимента или превышает ее. В последнем случае возможно использование двух подходов для определения границ интервалов. С теоретической точки зрения наиболее правильно использовать полученное значение h для построения интервалов. Такой подход не внесет дополнительных искажений, связанных с обработкой экспериментальных данных. Однако для практических целей в статистических исследованиях, относящихся к физической культуре и спорту, принято округлять полученное значение h до точности измерения данных. Связано это с тем, что для наглядного представления получаемых результатов удобно, чтобы границами интервалов являлись возможные значения признака. Таким образом, полученное значение ширины интервалов следует округлить с учетом точности проводимого эксперимента. Особо отметим, что округление необходимо производить не в общепринятом математическом смысле, а в сторону увеличения, т.е. с избытком, чтобы не уменьшить общий диапазон варьирования признака - сумма ширины всех интервалов не должна быть меньше разности между максимальным и минимальным значениями признака. В рассматриваемом примере экспериментальные данные определены с точностью до сотых (0,01 м), поэтому полученное выше значение ширины интервалов следует округлить с избытком с точностью до сотых. В результате получаем:
h= 0,67 (м).
После определения ширины интервалов группировки следует определить их границы. Нижнюю границу первого интервала целесообразно принять равной минимальному значению признака в выборке xmin:
xН1= xmin.
В рассматриваемом примере xН1= 13,04 (м).
Для получения верхней границы первого интервала (xВ1) следует к значению нижней границы первого интервала прибавить значение ширины интервала:
xВ1= хН1+h.
Заметим, что верхняя граница каждого интервала (здесь – первого) будет являться одновременно и нижней границей следующего (в данном случае второго) интервала: xН2= xВ1.
Подобным образом определяются значения нижних и верхних границ всех оставшихся интервалов:
xВi=xНi+1= xНi+h.
В рассматриваемом примере:
xВ1= xН2= xН1+h=13,04+0,67=13,71 (м),
xВ2= xН3= xН2+h=13,71+0,67=14,38 (м),
xВ3= xН4= xН3+h=14,38+0,67=15,05 (м),
xВ4= xН5= xН4+h=15,05+0,67=15,72 (м),
xВ5= xН5+h=15,72+0,67=16,39 (м).
Перед группировкой вариант введем понятие срединного значения интервала xi, равного значению признака, равноудаленного от концов этого интервала. Учитывая, что оно отстоит от нижней границы на величину, равную половине ширины интервала, для его определения удобно воспользоваться соотношением:
xi= xНi+ h/2,
где xНi - нижняя граница i-ro интервала, а h - его ширина. Срединные значения интервалов будут использоваться в дальнейшем при обработке сгруппированных данных.
После определения границ всех интервалов следует распределить выборочные варианты по этим интервалам. Но предварительно следует решить вопрос о том, к какому интервалу отнести значение, находящееся в точности на границе двух интервалов, т. е. когда значение варианты совпадает с верхней границей одного и нижней границей соседнего с ним интервала. В таком случае варианта может быть отнесена к любому из двух соседних интервалов и, для исключения неоднозначности при группировке, условимся в таких случаях относить варианты к верхнему интервалу. В пользу такого подхода можно привести следующий довод. Поскольку минимальное значение признака совпадает с нижней границей первого интервала и входит в этот интервал, то варианту, попадающую на границу двух интервалов, следует отнести к тому из них, значение нижней границы которого равно рассматриваемой варианте.
Перейдем к рассмотрению статистической таблицы - см. таблицу 4, которая состоит из семи столбцов.
Таблица 4
Табличное представление результатов в толкании ядра
| 4 | ||||||
| Номер интервала | Границы интервала | Срединное значение интервала | Частота | Накопленная частота | Частость | Накопленная частость |
| i | xНi – xВi | xi | ni | Ni | fi | Fi |
| 13,04 – 13,71 13,71 – 14,38 14,38 – 15,05 15,05 – 15,72 15,72 – 16,39 | 13,375 14,045 14,715 15,385 16,055 | 0,138 0,276 0,345 0,172 0,069 | 0,138 0,414 0,759 0,931 | |||
| Сумма |
В первых трех столбцах статистической таблицы содержатся соответственно номера интервалов группировки i, их границы xНi - xВi и срединные значения интервалов xi.
В четвертом столбце располагаются частоты интервалов. Частотой интервала называется число, показывающее сколько вариант, т.е. результатов измерений попало в данный интервал. Для обозначения этой величины принято использовать символ ni. Сумма всех частот всех интервалов всегда равна объему выборки п,что можно использовать для проверки правильности проведенной группировки.
Пятый столбец таблицы 4 предназначен для занесения в негонакопленной частоты интервала - числа, полученного суммированием частоты текущего интервала с частотами всех предыдущих интервалов. Накопленную частоту принято обозначать латинской буквой Ni. Накопленная частота показывает, сколько вариант имеют значения не больше, чем верхняя граница интервала.
В шестой столбец таблицы помещается частость. Частостью называется частота, представленная в относительном выражении, т.е. отношение частоты к объему выборки. Сумма всех частостей всегда равна 1. Для обозначения частости используется символ fi:
fi=ni/n.
Частость интервала связана с вероятностью попадания случайной величины в этот интервал. Согласно теореме Бернулли, при неограниченном увеличении числа опытов частость события сходится по вероятности к его вероятности. Если понимать под событием попадание значения исследуемой величины в определенный интервал, то становится ясно, что при большом числе опытов частость интервала приближается к вероятности попадания измеряемой случайной величины в этот интервал.
И частота, и частость характеризуют повторяемость результатов в выборке. Сравнивая их статистическое значение, следует отметить, что информативность частости существенно выше, чем у частоты. Действительно, если, как, например, в таблице 4 частота второго интервала равна 8 и, значит, 8 результатов попало в этот интервал, то трудно понять - мало это или много; если в выборке 1000 вариант, то такая частота мала, а если 20, то велика. В таком случае для объективной оценки необходимо сопоставить значение частоты с объемом выборки. Если же воспользоваться частостью, то сразу можно сказать, какая доля результатов попала в рассматриваемый интервал (примерно 28% в приведенном примере). Поэтому частость дает более наглядное представление о повторяемости признака в выборке. Особо следует отметить другое важное достоинство частости. Ее использование позволяет сопоставлять выборки различного объема. Частота для таких целей не применима.
В седьмом столбце таблицы расположена накопленная частость. Накопленной частостью является отношение накопленной частоты к объему выборки. Накопленная частость обозначается буквой Fi:
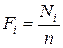 .
.
Накопленная частость показывает, какая доля вариант выборки имеет значения, не превосходящие значения верхней границы интервала.
Последняя строка статистической таблицы используется для контроля над проведением группировки.
После заполнения таблицы вернемся к определению статистического ряда. Как правило, статистический ряд оформляется в виде таблицы, в первой строке которой перечислены интервалы, а во второй – соответствующие им частости или частоты. Таким образом, статистическим рядом называется двойной числовой ряд, устанавливающий связь между численным значением исследуемого признака и его повторяемостью в выборке. Существенным достоинством статистических рядов является то, что они, в отличие от статистических совокупностей, дают наглядное представление о характерных особенностях варьирования признаков.
Дата добавления: 2015-01-15; просмотров: 2044;
