Вихідні ПОЛОЖЕННЯ ХВЛЬОВОЇ ОПТИКИ
1. Змінні електричні та магнітні поля, що поширюються в просторі, являють собою електромагнітні хвилі. На рис. 1 схематично показана електромагнітна хвиля, що поширюється в позитивному напрямку осі абсцис; E і H — відповідно вектори напруженості електричного та магнітного полів електромагнітної хвилі. Як видно з рис. 1, електромагнітні хвилі відносяться до класу поперечних хвиль, оскільки в них напрямки коливань векторів E і Hнормальні відносно вектора швидкості хвилі.
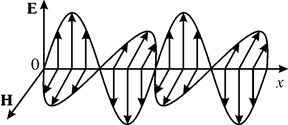 рис. 1
рис. 1
|
2. Світловими хвилями є електромагнітні хвилі з довжинами хвиль, що лежать у межах 400…760 нм. Кольорова характеристика світлової хвилі визначається довжиною хвилі (400 нм — фіолетовий колір, 760 нм — червоний колір). В тому випадку, коли світлові хвилі мають одну й ту ж саму довжину хвилі, світло називається монохроматичним. Якщо ж у світловому пучку перебувають усі довжини хвиль у межах від 400 до 760 нм (усі «кольору»), світло є білим.
3. Взаємодія світлової електромагнітної хвилі з речовинами в переважній більшості випадків визначається дією електричного поля хвилі, яка характеризується вектором напруженості електричного поля E. Надалі будемо називати E електричним (або світловим) вектором і в подальшому будемо абстрагуватися від дії магнітного поля світлової хвилі.
Важливою характеристикою світлової хвилі є її енергія (інтенсивність світла), пропорційна |E|2.
4. Поширення світла в просторі будемо описувати за допомогою понять «фронт світлової хвилі» і «світловий промінь».
Фронтом світлової хвилі називається геометричне місце точок простору, до яких досягла у цей момент часу світлова хвиля.
Світловими променями називаються прямі лінії, що виходять із джерела світла. Промені завжди перпендикулярні до фронту хвилі. й визначають напрямок переносу енергії світлової хвилі.
5. У вакуумі світлові хвилі поширюються зі швидкістю 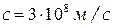 , а в речовині зі швидкістю
, а в речовині зі швидкістю  , де
, де 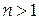 — показник заломлення, значення якого визначається конкретними властивостями речовини. При проходженні світлової хвилі в речовині її частота залишається незмінною, а довжина хвилі зменшується в
— показник заломлення, значення якого визначається конкретними властивостями речовини. При проходженні світлової хвилі в речовині її частота залишається незмінною, а довжина хвилі зменшується в  разів. Дійсно
разів. Дійсно
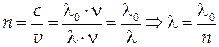
|
Тут 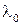 — довжина світлової хвилі у вакуумі,
— довжина світлової хвилі у вакуумі,  – її частота).
– її частота).
6. Світлові хвилі випускаються окремими атомами джерела світла незалежно одна від одної, тому початкові фази їх коливань не зв'язані між собою й з рівною ймовірністю довільно змінюються в часі. Такі хвилі називаються некогерентними й при накладенні в одній точці простору їх інтенсивності просто підсумовуються.
Когерентними називаються такі хвилі, які мають однакову частоту й не залежну від часу різницю фаз.
За допомогою певних пристроїв (див. нижче) можна виділити групи монохроматичних світлових хвиль, у яких різниця початкових і кінцевих фаз залишається постійною за часом, тобто такі хвилі будуть когерентними.
1.2 Інтерференція світлових хвиль
1. Явище накладення когерентних хвиль, в результаті якого відбувається просторовий перерозподіл інтенсивності, - виникає система інтерференційних максимумів і мінімумів, - називається інтерференцією.
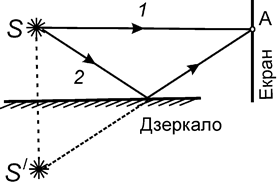 Рис. 2
Рис. 2
|
Для одержання когерентних хвиль світлову хвилю розщеплюють на дві (або більше) когерентні частини, а потім зводять їх знову разом, спостерігаючи інтерференційну картину.
Одна з найпростіших схем одержання двох когерентних світлові пучків (дзеркало Ллойда) показана на рис. 2. У точціі А на екрані інтерферують дві когерентні світлові хвилі, що випускаються дійсним джерелом світла S. і його уявним зображенням – S/. Перша хвиля падає на екран безпосередньо, а друга приходить у ту ж точку, відбившись від дзеркала.
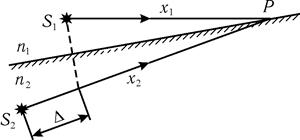
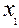 Рис.3 Рис.3
|
2. З'ясуємо умови виникнення інтерференційних максимумів або мінімумів у випадку інтерференції хвиль від двох когерентних джерел 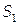 і
і  (рис. 3)
(рис. 3)
В точку Р, розташовану на границі розділу двох середовищ з показниками заломлення 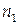 і
і  , від джерел
, від джерел 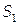 і
і  доходять світлові хвилі, рівняння яких мають вигляд
доходять світлові хвилі, рівняння яких мають вигляд
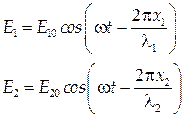
| (1) |
Тут 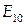 і
і  – амплітудні значення векторів напруженості електричної складової світлової хвилі, а довжини хвиль
– амплітудні значення векторів напруженості електричної складової світлової хвилі, а довжини хвиль 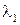 і
і 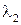 можна виразити через довжину хвилі
можна виразити через довжину хвилі 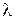 у вакуумі:
у вакуумі:

| (2) |
З (1) видно, що різниця фаз коливань, що додаються, дорівнює
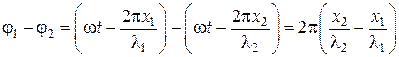 .
.
Скориставшись виразом (2), можна записати
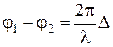
| (3) |
.
Різниця 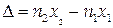 називається оптичною різницею ходу.
називається оптичною різницею ходу.
У точці Р складаються гармонічні коливання однакового напрямку 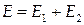 , при цьому результуюче коливання також буде гармонічним. Результуюча амплітуда такого коливання знайдеться за відомою формулою
, при цьому результуюче коливання також буде гармонічним. Результуюча амплітуда такого коливання знайдеться за відомою формулою
 , ,
| (4) |
Розглянемо окремі випадки.
1. Оптична різниця ходу дорівнює цілому числу півхвиль:
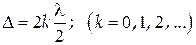
| (5) |
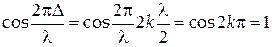 ; ;
| |
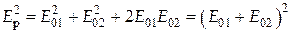 ; ;
| |
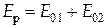 . .
| (6) |
З (6) видно, що в цьому випадку результуюча амплітуда коливань дорівнює сумі амплітуд, тобто відбувається взаємне посилення коливань і інтенсивності.
Таким чином, якщо оптична різниця ходу дорівнює парному числу довжин півхвиль, то виникає інтерференційний максимум. У цьому випадку світлові хвилі зустрічаються з однаковою фазою й взаємно підсилюють одна одну.
2. Оптична різниця ходу дорівнює непарному числу півхвиль:

| (7) |
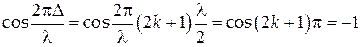 ; ;
| |
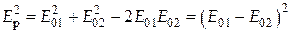 ; ;
| |
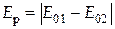 . .
| (8) |
З (8) видно, що результуюча амплітуда коливань дорівнює різниці амплітуд, тобто відбувається взаємне ослаблення амплітуд коливань. Якщо ж E01 = E02, то відбувається повне гасіння, тобто Ep = 0.
Таким чином, якщо оптична різниця ходу дорівнює непарному числу довжин півхвиль, то виникає інтерференційний мінімум. У цьому випадку світлові хвилі зустрічаються з протилежною фазою і взаємно послаблюють одна одну.
1.3 Інтерференція світла в тонких плівках
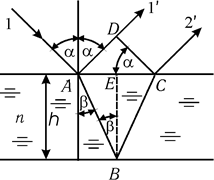 Рис.4
Рис.4
|
Важливим у практичному відношенні випадком інтерференції світлових хвиль є інтерференція світла в тонких плівках.
Нехай на поверхню розташованої в повітрі тонкої прозорої плівки товщиною h і з показником заломлення n падає світловий промінь (рис. 4). У точці A світловий промінь частково відбивається (промінь 1') і частково заломлюється. Заломлений промінь відбивається в точці B і повертається назад — промінь 2'. Промені 1' і 2' когерентні, оскільки вони утворилися в результаті поділу одного й того ж самого падаючого променя. Оптична різниця ходу між ними
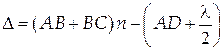 . .
| (7) |
Необхідність врахування додаткового доданка 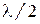 пов'язана з тим, що умови відбиття світлових променів у точках A і B різні. У точці A відбиття відбувається від оптично більш щільного середовища (з більшим показником заломлення); при цьому фаза світлової хвилі змінюється на
пов'язана з тим, що умови відбиття світлових променів у точках A і B різні. У точці A відбиття відбувається від оптично більш щільного середовища (з більшим показником заломлення); при цьому фаза світлової хвилі змінюється на 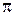 , що еквівалентно різниці ходу
, що еквівалентно різниці ходу 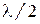 . У точці B світлова хвиля відбивається від оптично менш щільного середовища і її фаза при цьому не змінюється.
. У точці B світлова хвиля відбивається від оптично менш щільного середовища і її фаза при цьому не змінюється.
З рис. 4 видно, що
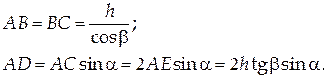
Підставивши ці вирази в (25.9) і замінивши за допомогою закону заломлення 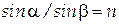 кут заломлення
кут заломлення 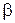 на кут падіння
на кут падіння 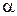 , після нескладних перетворень одержимо
, після нескладних перетворень одержимо
 . .
| (8 |
З (8) видно, що оптична різниця ходу залежить від трьох параметрів: товщини плівки h, кута падіння 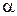 й довжини хвилі
й довжини хвилі 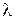 , тобто
, тобто 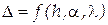 . Для аналізу результату інтерференції розглянемо окремі випадки, коли один з параметрів — змінний, а інші фіксовані.
. Для аналізу результату інтерференції розглянемо окремі випадки, коли один з параметрів — змінний, а інші фіксовані.
1. Нехай 
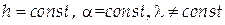 , тобто на плівку постійної товщини під одним і тим же кутом падає біле світло. Тоді, залежно від довжини хвилі, буде виконуватися або умова максимуму (5), або умова мінімуму (7). Внаслідок цього плівка у відбитому світлі буде пофарбованою – будуть видні ті кольори (ізохроми), яким відповідають довжини хвиль, що задовольняють умові максимуму. Додаткові кольори буде видні в прохідному світлі: цим кольорам відповідають довжини хвиль, які задовольняють умові мінімуму у відбитому світлі й умові максимуму в прохідному світлі.
, тобто на плівку постійної товщини під одним і тим же кутом падає біле світло. Тоді, залежно від довжини хвилі, буде виконуватися або умова максимуму (5), або умова мінімуму (7). Внаслідок цього плівка у відбитому світлі буде пофарбованою – будуть видні ті кольори (ізохроми), яким відповідають довжини хвиль, що задовольняють умові максимуму. Додаткові кольори буде видні в прохідному світлі: цим кольорам відповідають довжини хвиль, які задовольняють умові мінімуму у відбитому світлі й умові максимуму в прохідному світлі.
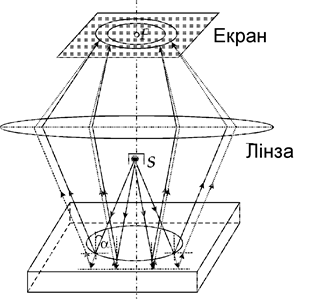 Рис. 5
Рис. 5
|
2. Нехай 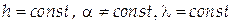 , тобто на плівку постійної товщини під різними кутами падає монохроматичне світло. У цьому випадку на плівці у відбитому світлі будуть видні світлі й темні смуги. Ці смуги називаються лініями постійного нахилу, оскільки кожна з них проходить по таких місцях плівки, де кут падіння один і той же: світлі смуги відповідають кутам нахилу, що задовольняють умові максимуму, темні — умові мінімуму. Різним лініям відповідають різні, але постійні кути падіння. Якщо джерело точкове, то на плівці будуть видні концентричні темні й світлі кола (рис. 5).
, тобто на плівку постійної товщини під різними кутами падає монохроматичне світло. У цьому випадку на плівці у відбитому світлі будуть видні світлі й темні смуги. Ці смуги називаються лініями постійного нахилу, оскільки кожна з них проходить по таких місцях плівки, де кут падіння один і той же: світлі смуги відповідають кутам нахилу, що задовольняють умові максимуму, темні — умові мінімуму. Різним лініям відповідають різні, але постійні кути падіння. Якщо джерело точкове, то на плівці будуть видні концентричні темні й світлі кола (рис. 5).
3. Нехай 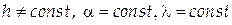 , тобто на плівку змінної товщини під одним і тим же кутом падає монохроматичне світло. На плівці будуть видні темні й світлі смуги, кожна з яких проходить по таких її місцях, де товщина одна й та сама (лінії рівної товщини). Різним лініям відповідають різні, але постійні товщини. Якщо, наприклад, взяти дротовий каркас із мильною плівкою й поставити його вертикально, то за рахунок стікання рідини вона придбає форму клина і на ній будуть видні горизонтальні світлі й темні смуги.
, тобто на плівку змінної товщини під одним і тим же кутом падає монохроматичне світло. На плівці будуть видні темні й світлі смуги, кожна з яких проходить по таких її місцях, де товщина одна й та сама (лінії рівної товщини). Різним лініям відповідають різні, але постійні товщини. Якщо, наприклад, взяти дротовий каркас із мильною плівкою й поставити його вертикально, то за рахунок стікання рідини вона придбає форму клина і на ній будуть видні горизонтальні світлі й темні смуги.
Явище інтерференції світла в тонких плівках лежить в основі просвітління оптики. Сучасні оптичні прилади (об'єктиви фотоапаратів, біноклі, секстанти, перископи і т.д.) містять велику кількість оптичних елементів (лінз, призм і т.п.). Проходження світла через кожний з таких елементів супроводжується частковим відбиттям, що може привести до істотної (до 40 %) втрати інтенсивності. Для зменшення втрат на відбиття на поверхню оптичних елементів наносять тонку плівку речовини, підбираючи її товщину так, щоб різниця ходу відбитих променів задовольняла умові мінімуму. Крім того, як показують теоретичні розрахунки, для повного гасіння відбитих променів необхідно підібрати плівку з показником заломлення, рівним кореню квадратному з показника заломлення скла. При виконанні цих умов відбиття припиняється, що суттєво збільшує світлосилу оптичних приладів.
1.4 Кільця Ньютона
Кільця Ньютона являють собою окремий випадок інтерференції світла в тонких плівках. Кільця Ньютона спостерігаються в тому випадку, коли опукла поверхня лінзи малої кривизни стикається із плоскою поверхнею скляної пластики (рис.5, а).
Між лінзою й пластинкою міститься тонкий повітряний прошарок, що поступово товщає від центру до країв.
На лінзу зверху нормально падає пучок паралельних монохроматичних променів і світлові промені, відбиті від нижньої поверхні лінзи і від верхньої поверхні пластинки (рис.6а), інтерферують між собою. При спостереженні зверху видно картину концентрично розташованих темних і світлих кілець, як це схематично показано на рис.6,б.
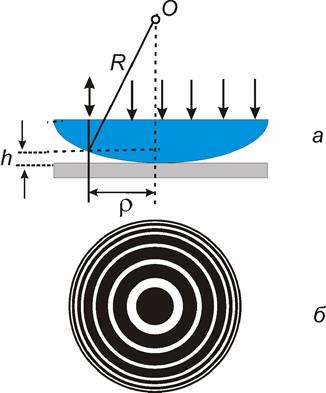 Рис.6.
Рис.6.
|
Для знаходження оптичної різниці ходу між променями, відбитими від верхньої й нижньої поверхні скористаємося формулою (8). У нашому випадку падіння променів нормально до поверхні лінзи, тому 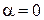 і, отже,
і, отже,  Крім того, слід урахувати, що при відбитті променя від нижньої границі лінзи показник заломлення повітря дорівнює одиниці
Крім того, слід урахувати, що при відбитті променя від нижньої границі лінзи показник заломлення повітря дорівнює одиниці 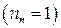 , тому відносний показник заломлення
, тому відносний показник заломлення 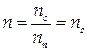 . Таким чином, формулу (8) у нашому випадку можна записати у вигляді:
. Таким чином, формулу (8) у нашому випадку можна записати у вигляді:
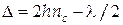
| (9) |
З формули (9) видне, що при 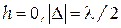 , тобто в центрі інтерференційної картини повинен спостерігатися мінімум, - темна пляма. З геометричних міркувань (рис.6, а) видно, що товщина повітряного прошарку
, тобто в центрі інтерференційної картини повинен спостерігатися мінімум, - темна пляма. З геометричних міркувань (рис.6, а) видно, що товщина повітряного прошарку 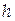 на деякій відстані
на деякій відстані 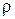 від центру, визначається формулою
від центру, визначається формулою
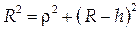
| (10) |
Оскільки 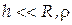 ,, то, нехтуючи
,, то, нехтуючи 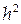 , після нескладних перетворень, одержимо:
, після нескладних перетворень, одержимо:
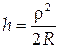
| (11) |
Умови виникнення інтерференційного мінімуму (темного кільця)
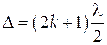
| (12) |
де 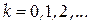 - номер темного кільця (відлік починають з центру).
- номер темного кільця (відлік починають з центру).
З (9), (11) і (12) одержимо
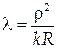
| (13) |
Таким чином, вимірявши радіус темного кільця Ньютона й знаючи радіус кривизни поверхні лінзи, можна розрахувати довжину світлової хвилі.
2.ЕКСПЕРИМЕНТАЛЬНА ЧАСТИНА
2.1. Ціль роботи.
Спостереження й вимір кілець Ньютона з наступним обчисленням значення довжини світлової хвилі, що пропускається світлофільтром.
2.2. Прилади й приналежності.
Джерело світла, фокусирующая лінза, система плосковыпуклой лінзи й скляної пластинки, світлофільтр, об'єктив.
2.3. Описання експериментальної установки.
 |
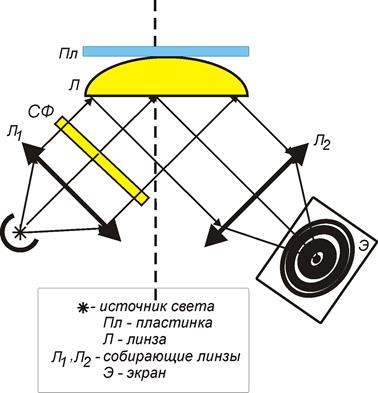 Рис.7
Рис.7
|
Для спостереження й виміру діаметрів кілець Ньютона в роботі використовується оптична установка, схема якої показана на рис.7. Від джерела світла й фокусуючої лінзи Л1 світлові промені направляються паралельним пучком на систему із плосковипуклої лінзи Л и скляної пластини Пл. Промені, відбиті від поверхні лінзи й пластини інтерферують між собою і об'єктив Л2 дає на екрані Э збільшене зображення інтерференційної картини кілець Ньютона. Світлофільтр СФ служить для монохроматизації світлових променів. Перед лінзою Л2 установлений металевий стрижень (на рисунку не показано), за допомогою якого визначають коефіцієнт збільшення оптичної системи.
2.4. Порядок проведення вимірів.
1.Після настроювання установки, лінійкою визначіть ширину „а” зображеного на екрані стрижня. Діаметр стрижня „в” зазначений на приладі. Значення „а” і „в” занесіть у таблицю.
2.Виміряйте діаметри п'яти кілець Ньютона. Для цього послідовно визначіть координати кінців діаметрів ліворуч і праворуч. Відлік починайте ліворуч від п'ятого кільця й далі, рухаючись до центру, проведіть виміру для наступних кілець менших номерів. Потім, пройшовши через центр, відзначайте координати правих кінців діаметрів кілець Ньютона. Для кожного кільця виміри проведіть три рази з точністю до 0,5 мм. Результати експерименту занесіть у таблицю. Радіус кривизни лінзи R зазначений на приладі.
Таблиця
Діаметр стрижня в= …… м.
Ширина зображення стрижня а=…….мм.
| № кільця | № досліду | Rлинзы= …….мм коэф. збільшення α=а/в=…… | ||||||
| відлік ліворуч N1, мм | відлік праворуч N2, мм | Дійсний
радіус. кільця
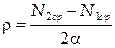
| ρ2 | λ нм | Δλ нм | (Δλ)2 (нм)2 | ||

| 
| 
| 
| 
| ||||
| ср | … | … |  … …
| … | … | … | … | |
| ср | … | … | … | … | … | … | … | |

| ||||||||

| 
| 
| 
| 
| ||||
| cp |

2.5. Обробка результатів вимірів.
1.По формулі α=а/в розрахуйте коефіцієнт збільшення.
2.Скориставшись виразом (13), проведіть розрахунок λ для кожного кільця.
3. По співвідношенню 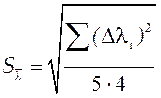 розрахуйте середню квадратичну похобку у визначенні
розрахуйте середню квадратичну похобку у визначенні 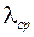 .
.
4.Остаточний результат запишіть у вигляді
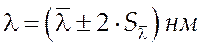
2.5.Приклад розрахунків.
Діаметр стрижня в=1,31 мм.
Ширина стрижня а=2,5 мм.
| № кільця | № досліду | Rлинзы= 3,23·103 мм коэф. збільшення α=а/в=1,91 | ||||||
| відлік ліворуч N1, мм | відлік праворуч N2, мм | Дійсний радіус. кільця | ρ2 | λ нм | Δλ нм | (Δλ)2 (нм)2 | ||
| 52,5 52,0 52,5 | 41,0 40,0 42,5 | 
| 
| 
| 
| 
| ||
| ср | 52,3 | 41,2 | 2,9 | 8,4 | 520,0 | |||

| 
| 
| 
| 
| ||||
| ср | 51,6 | 41,7 | 2,6 | 6,76 | 523,2 | 11,8 | 139,2 | |

| 
| 
| 
| 
| ||||
| ср | 51,2 | 42,4 | 2,3 | 5,3 | 546,9 | 11,9 | 141,6 | |
| . | 
| 
| 
| 
| 
| |||
| ср | 50,9 | 43,6 | 1,9 | 3,61 | 558,8 | 23,8 | 566,4 | |
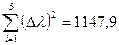
| 
| 
| 
| 
| 
| |||
| ср | 50,6 | 45,6 | 1,3 | 1,7 | 526,3 | 8,7 | 75,7 |
λср =535,0 нм 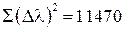
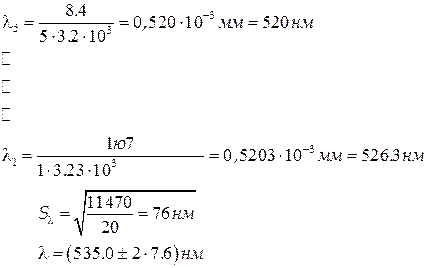
Контрольні питання.
1.У чому полягає явище інтерференції?
2.Виведіть умови виникнення інтерференційних максимумів і мінімумів.
3. Як утворюються кільця Ньютона?
4.Виведіть умову виникнення світлих кілець Ньютона.
Література.
1.Савельєв І.В. Курс общей физики. Т.2.с.338-340, 352-361, 1978 р.
2.Михайленко В.І., Белоус В.М., Поповський Ю.М. Загальна фізика. с 311-317.
Дата добавления: 2015-01-15; просмотров: 1295;
