Решение. а) Событие A – третьим по порядку будет черный шар.

а) Событие A – третьим по порядку будет черный шар.

Рассмотрим события:

A₁ = ббч – первый шар белый, второй шар белый, третий шар черный.

Аналогично:

A₂ = бчч; A₃ = чбч; A₄ = ччч.

Событие A произойдет, если произойдет любое из событий A₁, A₂, A₃, A₄:

A = A₁ + A₂ + A₃ + A₄.

Так как из урны последовательно достают все шары, то шары в урну не возвращают и при вычислении вероятности события A₁ = ббч рассчитываем условные вероятности того, что второй шар белый (при условии, что первый шар белый) и что третий шар черный (при условии, что первый шар белый и второй шар белый):

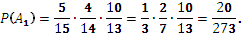
Аналогично:

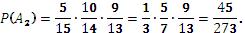
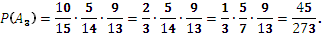
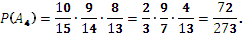
По теореме сложения вероятностей для несовместных событий:

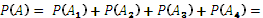
б) Пусть событие B – из первых трех шаров хотя бы один шар будет черным.

Противоположное событие:

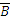– все три шара белые: .

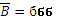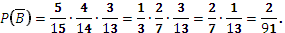
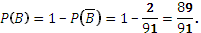
Ответ: а) ; б) .

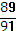3) В урне 5 белых, 10 черных и 5 красных шаров. Три из них вынимают наугад. Найти вероятность того, что по крайней мере два из них будут одноцветными. Шары в урну не возвращают.