ПРЯМОМ ИЗГИБЕ
При поперечном прямом изгибе, как это было сказано ранее, в поперечном сечении балки действуют внутренние силовые факторы - изгибающий момент Мх и перерезывающая сила Qy и соответствующие им нормальные а и касательные х напряжения.
Нормальные напряжения в произвольном слое сечения балки определяются по зависимости:
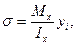(1)
где Мх - изгибающий момент в рассматриваемом сечении Мх>0; Iх - осевой момент инерции сечения; уi - расстояние от нейтральной линии (оси) до рассматриваемого слоя. Из зависимости (1) следует, что нормальные напряжения а по высоте сечения распределяются по линейному закону и достигают максимального значения в наиболее удаленных (опасных) от нейтральной линии точках сечения (рис. 3, а).
Для расчета на прочность определяется максимальное нормальное напряжение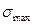 
в сечении, где действует максимальный изгибающий момент Мхmах. В этом случае, условие прочности будет иметь вид:
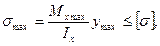(2)
где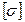 
- допускаемое нормальное напряжение.
В случае, если поперечное сечение балки симметрично относительно центральной линии (оси), условие прочности можно записать:
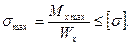(3)
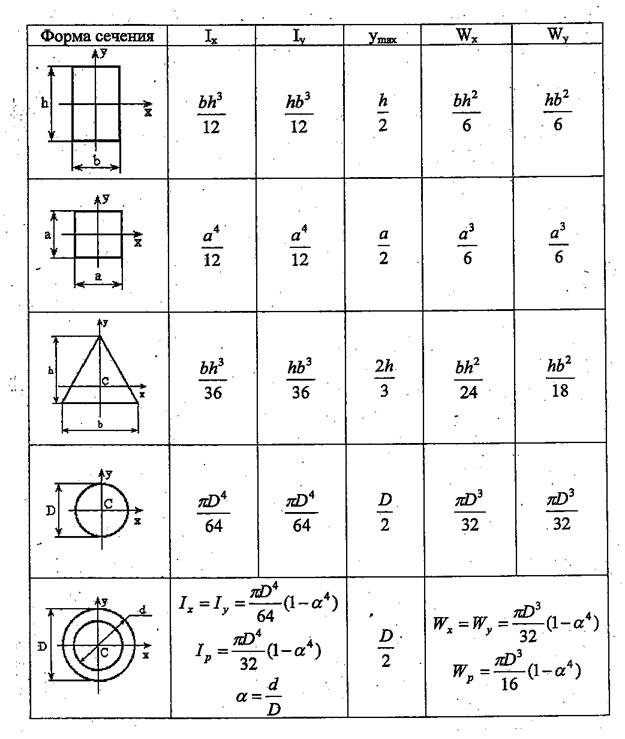
В этом случае экстремальные напряжения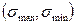 
будут по величине одинаковы, но разные по знаку (рис. 3, а), здесь Wx=Ix/ymax - осевой момент сопротивления. Осевой момент сопротивления Wx - это геометрическая характеристика плоского сечения, характеризующая влияние размеров и формы сеченияна максимальные нормальные напряжения. Для наиболее распространенных сечений балок геометрические характеристики приведены в таблице.
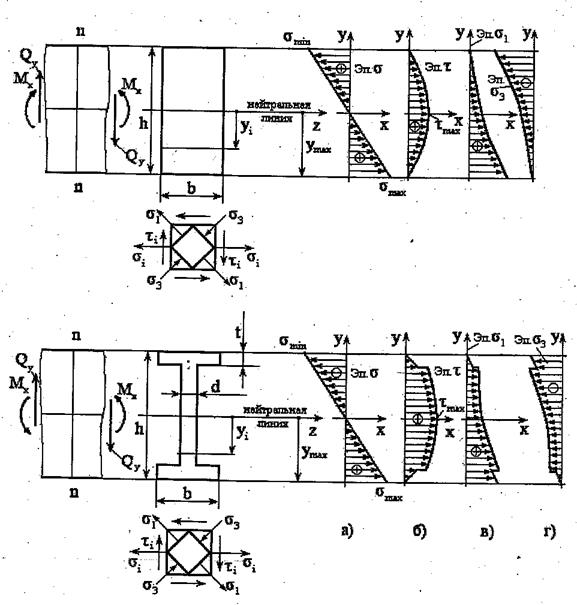
Рис. 3 Законы распределения нормальных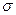 
(а), касательных 
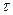(б) и
главных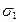 
(в),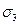 
(г) напряжений.
Для балок работающих на изгиб часто используют прокатные профили. Характерная особенность этих профилей - их экономичность. При одном и том же моменте сопротивления Wx площадь поперечного сечения прокатного сечения заметно меньше, чем площадь сплошного сечения.
Учащимся представляется возможность при выполнении проектного расчета балки сопоставить экономичность прокатного и сплошных сечений (прямоугольник, квадрат, круг, кольцевое сечение).
Дата добавления: 2015-03-26; просмотров: 1731;