Виды основных математических моделей строительного процесса.

Для обоснования оптимального варианта возведения зданий и сооружений требуются решения большого количества задач и выполнения вычислительных операций. К таким задачам относятся, например, выбор средств и орудий труда, выявление количественных зависимостей между параметрами строительно-технологического процесса, выбор оптимального состава процессов и т.д.

Основными факторами, которыми оперирует строительное производство, являются количество рабочих или машин (n) и продолжительность их деятельности (t), в течении которого они создают продукцию в количестве равном (V). Однако действие системы n→t→V позволяет оценить результат функционирования простого строительного процесса только для конкретных условий, что делает невозможным его оптимизацию. Этого можно достигнуть, если принять в качестве параметра оптимизации удельные затраты труда на единицу продукции.

Будем считать, что произведение n∙t есть фактические затраты труда Т_ф, тогда удельными затратами будет являться отношение фактических затрат труда к общему объему продукции произведенной в результате действия строительного процесса. Такие удельные затраты принято называть нормой времени, которая измеряется в человеко-часах (ч.час) или машино-часах (м.час.) на единицу продукции. То есть

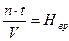
В связи с этим получаем уравнение равенства фактических и нормативных затрат труда, то есть Т_ф = Т_н, или, так называемое эргатическое (греч. ergates – действие) уравнение

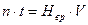(2.12)

Таким образом, любой строительный процесс и задачи, возникающие при разработке технологии возведения зданий и сооружений, представляют собой совокупность факторов различного происхождения, т.е. систему. В зависимости от устойчивости существования факторов, входящих в систему, их значимости, можно судить о надежности системы в целом. Системы можно разделить на два класса: детерминированные и стохастические.

Детерминированные системы объединяют процессы, которые взаимодействуют между собой точно предвиденным образом. Неопределенность отсутствует. Изменение одного из элементов системы на некоторую величину всегда вызывает изменение другого или других на строго определенную величину. Если Xi + DХ, то свойство Yi+ DY. Например: если увеличивается мощность потока, то сокращается срок производства работ.

Стохастические системы,или вероятностные, по своей природе непредсказуемы, Такие системы требуют тщательного исследования. Основной целью при этом является определение наибольшей степени вероятности поведения подобной системы в любых заданных условиях. В стохастических системах действуют случайности. То есть, если X +DХ, то элемент системы примет вид

R_i = R + DR + j,

где j - элемент случайности. Если под действием случайности j = - DR, то влияние X_i

на величину Ri вообще данным наблюдением обнаружено не будет.

Необходимо отметить, что понятие о детерминированных и стохастических системах отвечает известному положению о двух формах причинной связи явлений - наличие динамических и статистических закономерностей. Если классическим выражением динамического типа являются законы ньютоновской механики, то статистические закономерности точно и полно могут отражать свойства явлений только при сочетании множества элементарных и индивидуальных свойств. В этом случае можно будет утверждать, что они не зависят от воли и желания исследователя и распространяются на все явления одного типа.

Главное их применение состоит в предвидении свойств с определенной степенью вероятности. Управление подобными системами предполагает принятие обоснованных решений о том или ином выборе или изменении входных параметров. Выбор правильного решения из большого числа вариантов возможен при формализации процесса принятия решения и применении количественного описания альтернатив. После создания формализованной системы ее можно анализировать с помощью ЭВМ, куда вводится математическая модель поведения системы.

Математической моделью (ММ) называют описание системы на формальном языке, позволяющее выводить суждение о некоторых чертах поведения этой системы при помощи формальных процедур над ее описанием.

В зависимости от того, какие стороны объекта представлены в модели, возможны следующие их разновидности: субстанциональные, структурные и функциональные. Как те, так и другие модели они могут быть созданы в рамках как детерминированных, так и стохастических систем.

Субстанциональные модели (вещество, субстанция) формируются при исследовании материалов, совпадающие с материалом оригинала. Например: по результатам испытания бетонных образцов составляют представление о работе всей железобетонной конструкции и т.д.

Структурные модели имитируют внутреннюю структуру оригинала. Как правило, это модели со статистической структурой, Они создаются на основании значительного количества экспериментов и результатов их анализа. К ним относится технологическая схема производства бетона, схема размещения арматуры в железобетонных конструкциях, способ укладки зерен заполнителя с различной фракцией в массе бетонной смеси, строительно-технологический процесс возведения зданий и сооружений, задачи оптимизации транспортных потоков, структура межотраслевых связей предприятия и т.д.

Функциональные модели имитируют способ поведения оригинала. Они наиболее распространены в современной науке. Подобные модели предусматривают формализацию процесса в полном объеме системы. Однако при этом приходится учитывать все существующие связи системы, которые иногда составляют большое число. Вместе с тем, такой подход к решению задач оказывается возможным благодаря большой разрешающей способности современных ЭВМ и их быстродействию. Абстрактным образом функциональной модели принято считать «черный ящик», внутренняя структура которого неизвестна. Рис. 2,4.

		y

Рис. 2.4. Схема « черного ящика».

В этом случае задача управления сводится к подбору таких уровней X, которые обеспечили бы оптимальное значение У. В результате исследования значений X и соответствующие им значения У находят статистическую закономерность. При этом часто абстрагируются от некоторых сложных и пока мало изученных явлений. Путем последовательных операций (итераций) приближаются к истине.

В результате количественного исследования функциональной модели «черного ящика» удается получить совокупность соотношений, которые в виде математических зависимостей выражают реальные физические характеристики систем. Это могут быть графики, уравнения, неравенства, логические условия или графы и т.д. Такая совокупность соотношений вместе с условиями, ограничивающие пределы изменения физических характеристик, позволяет построить математическую модель.