Некоторые методы построения математических моделей строительных процессов.
Построение математических моделей, в основном, осуществляют или путем анализа количественных зависимостей качественных параметров строительных процессов с помощью методов математической статистики, или путём экстремального планирования экспериментов при поиске оптимальных условий. При анализе количественных зависимостей находят корреляционную взаимосвязь технологических факторов, что позволяет создать математическую модель.
Допустим, что необходимо найти зависимость производительности труда плотников ( П) при установки опалубки для монолитных железобетонных конструкций от затрат труда Т на исправление дефектов. Рис. 2.5.
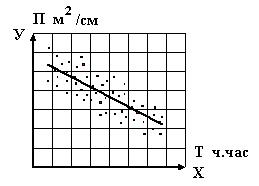
Рис. 2.5. Корреляционное поле П = f(Т)
При анализе корреляционного поля можно допустить, что математическая зависимость может быть описана уравнением
Y = A – C X (2.13)
С помощью метода наименьших квадратов определяют коэффициенты предполагаемого уравнения «А» и «С». С этой целью определяют средние значения X и Y.
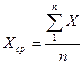 и
и 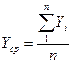 ;
;
где n – число парных наблюдений. Далее рассчитывают средние квадратичные отклонения
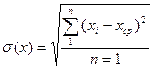
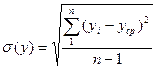 (2.14)
(2.14)
Достоверность результатов при соответствующем количестве парных корреляций устанавливают с помощью коэффициента корреляции:
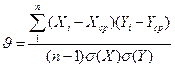
 (2.15.)
(2.15.)
В настоящее время для решения или оптимизации подобных детерминированных математических моделей разработано большое количество программ, позволяющих с помощью ЭВМ устанавливать приемлемость или достоверность того или иного уравнения. Однако несколько иначе обстоит дело с разработкой математической модели, когда приходится рассматривать одновременно два и более факторов. В этом случае, наиболее удобным методом создания математической модели может быть метод экстремального планирования экспериментов. Он позволяет не только найти адекватное математическое описание строительного процесса, но и провести его количественный анализ.
Для формального математического описания процесса применяют методы математической статистики. К ним относятся методы экстремального планирования экспериментов, позволяющие получить с заданной достоверностью уравнения зависимостей и провести их оптимизацию. Методы подразумевают экстремальное накопление информации, полученной непосредственно с действующего объекта, с ее последующей обработкой.
Планирование эксперимента - это процедура выбора числа и условия проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Для этого необходимо соблюдать определенные условия:
- Общее количество опытов или наблюдений должно быть минимальным.
- Должна быть обеспечена возможность одновременного варьирования всеми переменными, определяющими строительный процесс, по соответствующему алгоритму.
- Используемый математический аппарат должен позволять формализовать действия экспериментатора.
- При проведении экспериментов необходимо иметь возможность выбора решения при анализе каждой отдельной серии.
Поиск оптимальных условий является одной из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения эксперимента и необходимо найти наилучшие условия его реализации.
Эксперимент, который проводится для решения задач оптимизации, называют экстремальным. При этом задача является экстремальной, если цель ее состоит в поиске экстремума некоторой функции. Все переменные в решаемой задаче или способы воздействия на систему обозначают буквой (X) и называют факторами. Результаты их воздействия оцениваются параметром оптимизации (У), так называемой функцией отклика. Под математической моделью понимают уравнение, связывающее параметр оптимизации с факторами. В общем, виде уравнение может быть записано как
У = f(X1 X2 X3........Xn) (2.16)
Каждый фактор может принимать в опыте одно из нескольких значений, которые называют уровнями. Поэтому при планировании экспериментов преследуют определенную цель: перебрать все возможные наборы состояния системы, полное множество различных состояний. Это обстоятельство определяет возможное число опытов. С цель снижения их количества эксперименты планируют.
Эксперимент, предполагающий активное вмешательство в процесс и возможность выбора в каждом опыте тех уровней факторов, которые, по мнению экспериментатора наиболее важны, называют активным. Однако управляемых объектов не существует, так как на реальный объект воздействуют как управляемые, так и не управляемые факторы.
Поэтому, если невозможно воспроизвести эксперимент, то применяют метод пассивного эксперимента, что фактически означает статистическую обработку полученных результатов.
При планировании экстремального эксперимента очень важно определить параметр оптимизации. Им может быть признак, по которому оптимизируется процесс. Он должен быть количественным и задаваться числом. Его необходимо уметь измерять. Наиболее часто каждый фактор изменяют в двух уровнях (нижний - min и верхний - max). Интервалом варьирования факторов называют число, прибавление которого к основному уровню(нулевому) образует верхний, а вычитание – нижний уровень. Для упрощения записи условий эксперимента и обработки результатов исследований масштабы по осям преобразования факторов выбирают так, чтобы верхний уровень соответствовал (+1), нижний (- 1), основной - (0). Для факторов с непрерывной областью определения это всегда можно сделать с помощью следующих 
преобразований
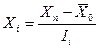 (2.17)
(2.17)
где Xi - кодированное значение фактора; Xn - натуральное его значение;`X0 - натуральное значение основного (нулевого) уровня; Ii - интервал варьирования.
При двух уровнях варьирования число опытов N может быть определено как
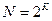
где к - количество факторов.
На основании этого составляется матрица планирования экспериментов, учитывающая все возможные сочетания «+» и «-» . Табл. 2.1.
Таблица 2.1.
Матрица планирования двух факторного эксперимента
| Номер опыта | Х0 | Х1 | Х2 | Х12 | Функция отклика Y |
| +1 | -1 | -1 | +1 | Y1 | |
| +1 | +1 | -1 | -1 | Y2 | |
| +1 | -1 | +1 | -1 | Y3 | |
| +1 | +1 | +1 | +1 | Y4 |
В общем виде математическая модель может быть записана в виде
Y = B0X0 + B1X1 +B2X2 + B12X1X2 (2.17)
 |
Коэффициенты в уравнении определяются следующим образом

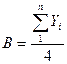 ;
; 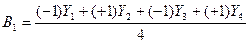 и т.д.
и т.д.
Математическая модель, представленная уравнением регрессии, включает в себя два фактора и графически может быть представлена в виде, как это показано на рис.2.6
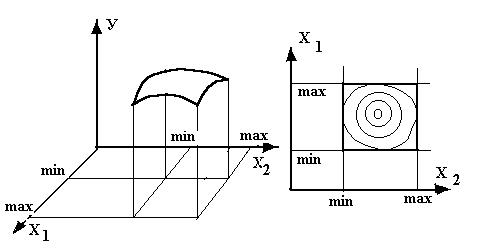
Рис. 2.6. Графическая интерпретация двухфакторного эксперимента.
В качестве примера можно рассмотреть задачу приготовления бетонной смеси, в которой рассматривается влияние конструктивных параметров смесителя на величину энергозатрат. В данном случае параметром оптимизации является удельное сопротивление, возникающее на поверхности лопасти при перемещении ее в массе бетонной смеси в зависимости от скорости вращения лопастей, их количества и расхода цемента в смеси, определяющего величину вязкого сопротивления смеси.
Таким образом, в качестве факторов были приняты:
Xi - количество лопастей с диапазоном варьирования от 3 до 6; Х2 - скорость вращения лопастей, изменяющаяся от 41 об/мин до 26 об/мин.; Х3 - расход цемента, необходимый для приготовления бетонной смеси с интервалом варьирования от 5ООкг/м3 до 250 кг/м3. Таблица 2.2.
Таблица 2.2.
Таблица варьирования уровней факторов
| Уровни | X1 | X2 | X3 |
| /+/ верхний | |||
| нулевой | 33,5 | ||
| /-/ нижний | |||
| интервал варьир. | 7,5 |
В соответствии с выражением N = 2k , где к = 3, общее количество опытов не должно быть меньше 8. При проведении экспериментов в соответствии с матрицей планирования, для каждого сочетания (+) и (-) были получены величины параметра оптимизации У. Таблица 2.3.
Таблица 2.3.
Матрица планирования и результаты исследования.
| №№ опытов | X0 | X1 | X2 | X3 | X1 X2 | X1 X3 | X2 X3 | X1X2X3 | У |
| + | - | - | + | + | - | - | + | 1,0 | |
| + | - | + | - | - | + | - | + | 0,85 | |
| + | + | - | - | - | - | + | + | 0,56 | |
| + | + | + | + | + | + | + | + | 0,9 | |
| + | - | - | - | + | + | + | - | 0,73 | |
| + | - | + | + | - | - | + | - | 1,1 | |
| + | + | — | + | - | + | - | - | 0,8 | |
| + | + | + | - | + | - | - | - | 0,66 | |
| Вi | 0,83 | -0,1 | 0,05 | 0,13 | -0,003 | -0,005 | -0,003 | -0,003 |
Таким образом, математическая модель была получена в виде уравнения регрессии, в котором знаки и коэффициенты регрессии указывают на степень значимости рассматриваемых факторов. В общем виде уравнение может быть записано следующим образом:
У = 0,83 - 0,lX1 + 0,05Х2 + 0,13Х3 - 0,003X1X2 - 0,006X1X3 - 0,ООЗХ2Х3 + 0,003X1X2X3.
В дальнейшем, на основании положения математической статистики и теории вероятности, необходима проверка значимости полученных коэффициентов и оптимизация уравнения.
Дата добавления: 2015-03-23; просмотров: 1509;
