Критерий подобия Рейнольдса, Фруда, Эйлера, Вебера

Критерий Ньютона Ne выражает зависимость между силами, массами, скоростями и линейными размерами в динамически подобных потоках в общем виде. В гидравлике приходится иметь дело главным образом с тремя видами сил: силой веса, силой давления и силой трения. В некоторых случаях приходится принимать во внимание силы поверхностного натяжения. При этом чаще всего в различных явлениях главную роль играет только один из этих видов сил. В общем, идеальном, случае полного подобия необходимо иметь подобие всех сил. Однако каждый их этих видов сил требует своих условий подобия, причем иногда несовместимых. Таким образом, удовлетворить основному условию подобия – равенству критериев Ньютона – не всегда возможно. В таких случаях необходимо обеспечить подобие того вида сил, который оказывается наиболее существенным в изучаемом явлении.

Критерии частичного подобия можно получить из критерия Ньютона, подставив в него, например, вместо силы F силу трения 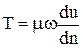, при этом получим условие подобия только сил трения (критерий Рейнольдса – Re), или силу тяжести G=mg – получим условие подобия только сил тяжести (критерий Фруда – Fr), или силу давления Р=р 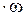- условие подобия только сил давления (критерий Эйлера – Eu).

Подставим в выражение (8.1) силу трения Т:

.

Имея в виду, что , а в подобных системах

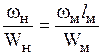и ,

будем иметь

,

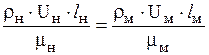где - критерий Рейнольдса.

Таким образом, подобие сил трения в потоках, удовлетворяющих условиям геометрического, кинематического и материального подобия, будет только в том случае, если для каждой пары соответственных точек потока натуры и модели число Рейнольдса будет иметь одно и то же значение. В числе Рейнольдса за величину U может быть принята средняя скорость потока V, а за l - любая характерная линейная величина. Например, при изучении законов движения жидкости в трубах применяется диаметр трубы d или гидравлический радиус R. При этом число Рейнольдса будет представлено в виде

; .

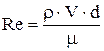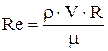Следует иметь в виду, что для подобия двух явлений существенно не численное значение критерия, а лишь его равенство для потоков натуры и модели.

Подставив в выражение (8.1) силу тяжести G = mg, получим

или после сокращения

,

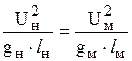где 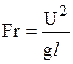- критерий (число) Фруда.

Иногда число Фруда выражают через среднюю скорость:

.

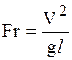Равенство числа Фруда (Fr) в соответствующих точках потоков, удовлетворяющих геометрическому, кинематическому и материальному подобию, обеспечивает подобие сил тяжести. За величину l может быть принята любая характерная линейная величина.

Подставив в выражение (8.1) силу давления Р = р 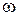, получим

.

Имея в виду, что и, кроме того, в геометрически подобных системах 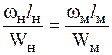, найдем

,

где 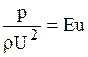- критерий (число) Эйлера.

Числу Эйлера придают несколько иной вид, введя вместо абсолютного давления р разность давления Δр:

.

Число Эйлера играет большую роль в исследовании явлений, связанных с кавитацией. В этом случае за Δp принимается Δp = p - р_п, где р_п – давление парообразования. Число k=2Еu называется числом кавитации. Таким образом, равенство чисел Эйлера обеспечивает в динамически подобных потоках подобие сил давления.

В некоторых гидравлических исследованиях существенное значение имеет поверхностное натяжение. Для получения соответствующих условий подобия можно также исходить из критерия Ньютона, подставляя в него значение силы поверхностного натяжения F= 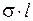, где σ - коэффициент поверхностного натяжения. Преобразования, не отличающиеся от предыдущих, позволяют получить число Вебера – критерий подобия сил поверхностного натяжения в виде

,

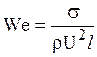где l - характерная линейная величина.