Идеальной жидкости. График уравнения Д.Бернулли

Это уравнение является основным в гидродинамике. Оно устанавливает связь между давлением, скоростью и положением жидкости в пространстве и может быть получено аналитически только для случая движения идеальной жидкости, т.е. жидкости, лишенной всех свойств реальной жидкости (абсолютно несжимаема и нерасширяема, а главное, абсолютно подвижна, т.е. лишена вязкости). Такой жидкости в природе не существует. Близок к ней жидкий гелий при температуре 2^оК.

Представим себе элементарную струйку переменного сечения (рис.4.8).

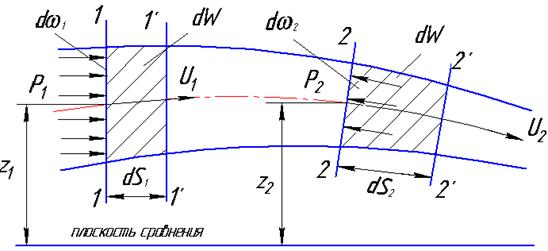
Рис.4.8

Двумя сечениями 1-1 и 2-2 с живыми сечениями d ₁ и d ₂ выделим отсек жидкости 1-1-2-2. допустим, что за бесконечно малое время dt этот отсек сдвинулся и занял новое положение 1'-1'-2'-2'. Живые сечения при этом переместились соответственно на расстояния ds₁ и ds₂.

Из рисунка 4.8 видно, что никакого изменения в пространстве не получил отсек жидкости 1'-1'-2-2, при движении он не совершил никакой работы, т.е. отсек жидкости 1-1-1'-1' с высоты Z₁ как бы переместился до высоты Z₂ и занял положение 2-2-2'-2' (на рисунке они заштрихованы).

На основании уравнения неразрывности делаем вывод, что массы жидкости в этих отсеках равны между собой, а скорость в сечении 2-2 по сравнению с сечением 1-1 возросла, т.е. произошло изменение кинетической энергии.

Для вывода этого уравнения используем известную из механики теорему об изменении кинетической энергии. Напомним, что эта теорема читается так:

изменение кинетической энергии 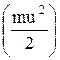рассматриваемого тела на некотором его перемещении равно сумме работ от внешних сил, приложенных к данному телу на том же перемещении.

Какие же силы действуют в нашем случае?

Это силы тяжести и силы давления. Согласно упомянутой выше теореме можно записать:

dT=A_G+A_p, (4.3)

где dT – изменение кинетической энергии; A_G - работа от сил тяжести; A_p - работа от сил давления.

Изменение кинетической энергии

dT= .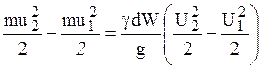

Работа от сил тяжести

.

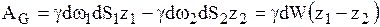Работа от сил давления

.

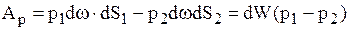Сделаем подстановку составляющих в выражение (4.3):

.

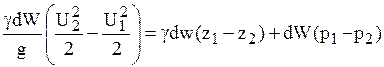
Разделим каждое слагаемое на 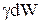и сгруппируем:

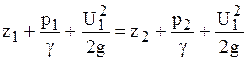. (4.4)

Выражение (4.4) является расчетной формой уравнения Бернулли, т.е. в такой форме оно составляется при решении различных задач.

. (4.5)

Выражение (4.5) является общей формой уравнения Бернулли.

Каждый из членов этого уравнения имеет линейную размерность и называется «напор», т.е. это удельная энергия, а удельная энергия – это энергия единицы веса жидкости, т.е. одного ньютона.

В формуле (4.5):

z– геометрический напор, или удельная потенциальная энергия положения;

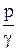- пьезометрический напор, или удельная потенциальная энергия давления;

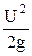- скоростной напор, или удельная кинетическая энергия.

Сумма перечисленных напоров составляет гидродинамический напор:

Н_г.д = z+ + .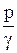

Физический смысл уравнения Бернулли заключается в том, что оно является уравнением закона сохранения энергии для движущейся жидкости.

Для лучшего понимания смысла полученного уравнения (4.4) представим его графически (рис.4.9).

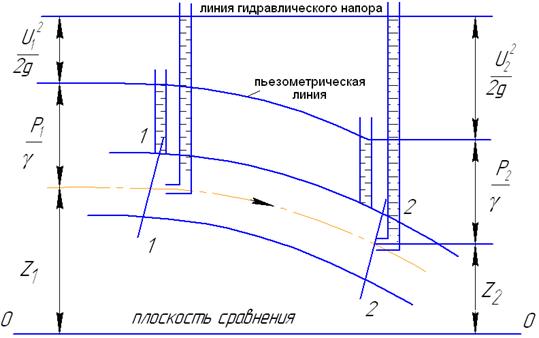
Рис.4.9