Основное уравнение равномерного движения

Равномерным движением называется установившееся движение, при котором скорости частиц жидкости не изменяются вдоль траекторий. При равномерном движении жидкости в водопроводах, а также в открытых руслах живые сечения, средние скорости течения и глубины по длине потока остаются постоянными.

Выведем основное уравнение равномерного движения, на основании которого выявим факторы, влияющие на величину гидравлических потерь по длине трубопровода.

Рассмотрим поток жидкости произвольной формы площадью 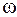, имеющий по длине постоянное живое сечение и наклоненный к горизонту под углом 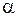(рис. 5.1). Выделим в потоке сечениями 1-1 и 2-2 отсек длиной l. Действие отброшенной жидкости слева и справа заменим давлениями р₁ и р₂, которые создают внешние силы, приводящие жидкость в движение: 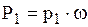; 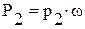. К ним относятся и сила тяжести отсека жидкости:

.

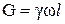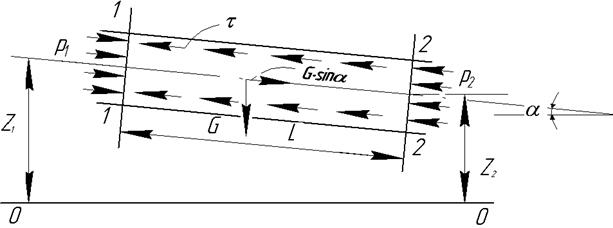
Рис.5.1

На жидкость действуют также силы сопротивления движению. Эти силы приложены вдоль поверхности стенок. Обозначим через 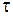удельную силу трения, через 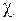– длину смоченного периметра. Тогда сила трения

.

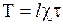Составим уравнение равновесия сил, действующих на выделенный отсек.

По условию равномерного движения, внешние силы, приводящие жидкость в движение, должны быть равны силам сопротивления, т.е. если спроектировать все силы на ось потока, получим

,

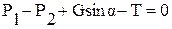где .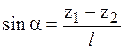

Тогда получим

.

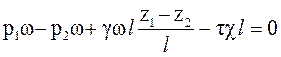Разделим все слагаемые на 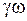и сгруппируем

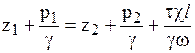. (5.1)

Сравним выражение (5.1) с уравнением Бернулли для потока реальной жидкости:

.

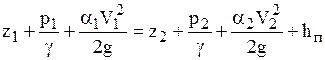Так как V₁ = V₂, то

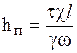. (5.2)

Так как 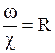- гидравлический радиус, то выражение (5.2) представим в виде

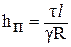. (5.3)

разделим левую и правую часть выражения (5.3) на l:

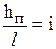или

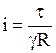. (5.4)

Выражения (5.2), (5.3) и (5.4) являются уравнениями равномерного движения.