Статические нагрузки двухконцевых лебедок
Для этого вида расчета должен быть полностью разработан рабочий чертеж вала.
Цель расчета: предотвращение усталостного разрушения вала в опасных сечениях в течение заданного срока службы.
6.3.1 Количественно цель расчета выражается формулой общего коэффи-циента запаса
S = Ss St / (Ss2 + Ss2)1/ 2 ³ [S] (6.12)_
где [S] = 1,5...2,5 в зависимости от ответственности конструкции, последствий разрушения, точности расчета нагрузок и напряжений, уровня технологии изготовления и контроля.
Коэффициенты запаса по нормальным Ss и касательным St напряжениям [1, c.169] :
Ss = s–1D / (sa + ysDsm) , St = t–1D / (ta + ytDtm) (6.13)
Нормальные напряжения изменяются по симметричному циклу (R = – 1,
sa = sИ , sm = 0), а касательные – по отнулевому (R = 0, ta = tm = tК / 2).
Тогда формулы (6.13) преобразуются к виду:
Ss = s–1D / sИ , St = 2t–1D / [tК (1 + ytD)] (6.14)
где напряжения в опасных сечениях равны
sa = sИ = 103М / W ; tК = 103T / WP (6.15)
(здесь расчет ведется на длительное число циклов нагружения, перегрузка на усталость не влияет; М – по формуле (6.6)) ;
s–1D, t–1D – пределы выносливости вала в рассматриваемом сечении :
s–1D = s–1 / KsD, t–1D = t–1 / KtD (6.16)
где s–1, t–1 – пределы выносливости образцов материала вала при симметри-чном цикле нагружения (таблица 1.1);
KsD, KtD – коэффициенты снижения пределов выносливости при переходе от образца материала к сечению реальной детали :
KsD = (Ks / Kds + 1/ KFs – 1) / KV ;
KtD = (Kt / Kdt + 1/ KFt – 1) / KV ; (6.17)
ytD = yt/ KtD – коэффициент влияния асимметрии цикла в рассматривае-мом сечении (yt - по таблице 1.1)_
В формулах (6.17) Ks и Kt - эффективные коэффициенты концентрации напряжений; Kds и Kdt - коэффициенты влияния абсолютных размеров поперечного сечения (таблица 6.1) ; KFs и KFt - коэффициенты влияния качества (шероховатости) поверхности (таблица 6.2) ; KV - коэффициент влияния поверхностного упрочнения (таблица 6.3)
Таблица 6.1 – Коэффициенты Kds и Kdt [1, c.170]
| Коэффициенты, материал | Kds и Kdt при диаметре вала d мм | ||||||
| Kds | для углеродистой стали | 0,92 | 0,88 | 0,85 | 0,81 | 0,76 | 0,71 |
| для легированной стали | 0,83 | 0,77 | 0,73 | 0,70 | 0,65 | 0,59 | |
| Kdt | для всех сталей |
Таблица 6.2 – Коэффициенты KFs и KFt [1, c.170]
| Вид механической обработки | Параметр | KFs при sВ, МПа | KFt при sВ, МПа | ||
| шероховатости Ra, мкм | £ 700 | > 700 | £ 700 | > 700 | |
| Шлифование тонкое | до 0,2 | ||||
| Обтачивание тонкое | 0,2...0,8 | 0,99...0,93 | 0,99...0,91 | 0,99...0,96 | 0,99...0,95 |
| Шлифование чмстовое | 0,8...1,6 | 0,93...0,89 | 0,91...0,86 | 0,96...0,94 | 0,95...0,92 |
| Обтачивание чистовое | 1,6...3,2 | 0,89...0,86 | 0,86...0,82 | 0,94...0,92 | 9,92...0,89 |
Таблица 6.3 – Коэффициент KV
| Вид упрочнения поверхности вала | З н а ч е н и я KV п р и | ||
| Ks =1,0 | Ks =1,1 1,5 | Ks ³ 1,8 | |
| Закалка ТВЧ | 1,3...1,6 | 1,6...1,7 | 2,4...2,8 |
| Цементация | 1,1...1,5 | 1,2...2,0 | 2,0...3,0 |
| Азотирование | 1,15...!.25 | 1,3...1,9 | 2,0...3,0 |
| Накатка роликом | 1,2...1,4 | 1,5...1,7 | 1,8...2,2 |
| Дробеструйный наклеп | 1,1...1,3 | 1,4...1,5 | 1,6...2,5 |
Значения эффективных коэффициентов концентрации напряжений следует принимать :
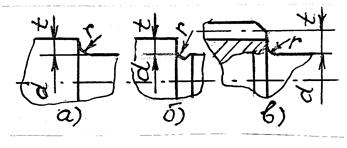
– для ступенчатого перехода участков вала с галтелью в соответствии с рисунком 6.3 – по таблице 6.4;
Рисунок 6.3 – Участки перехода вала с галтелью r | – для шпоночного паза, шлицевых и резьбовых участ-ков вала – по таблице 6.5; Для деталей, установленных на вал с натягом в расчетах используют отношения Ks / Kds, Kt / Kdt из таблицы 6.6 |
Таблица 6.4 – Коэффициенты Ks, Kt в галтелях вала [1, c.171]
| t / r | r / d | Ks при sВ, МПа | Kt при sВ, МПа | ||||||
| 0,01 | 1,55 | 1,6 | 1,65 | 1,7 | 1,4 | 1,4 | 1,45 | 1,45 | |
| 0,02 | 1,8 | 1,9 | 2,0 | 2,15 | 1,55 | 1,6 | 1,65 | 1,7 | |
| 0,03 | 1,8 | 1,95 | 2,05 | 2,25 | 1,55 | 1,6 | 1,65 | 1,7 | |
| 0,05 | 1,75 | 1,9 | 2,0 | 2,2 | 1,6 | 1,6 | 1,65 | 1,75 | |
| 0,01 | 1,9 | 2,0 | 2,1 | 2,2 | 1,55 | 1,6 | 1,65 | 1,75 | |
| 0,02 | 1,95 | 2,1 | 2,2 | 2,4 | 1,6 | 1,7 | 1,75 | 1.85 | |
| 0,03 | 1,95 | 2,1 | 2,25 | 2,45 | 1,65 | 1,75 | 1,75 | 1,9 | |
| 0,01 | 2,1 | 2,25 | 2,35 | 2,5 | 2,2 | 2,3 | 2,4 | 2,6 | |
| 0,02 | 2,15 | 2,3 | 2,45 | 2,65 | 2,1 | 2,15 | 2,25 | 2,3 |
Таблица 6.5 – Коэффициенты Ks, Kt для шпоночного паза, шлицев, резьбы [1, c.171]
| sВ, МПа | Шпоночный паз | Шлицы | Резьба | ||||||
| Ks при выполнении фрезой | Kt | Ks | Kt | Ks | Kt | ||||
| концевой | дисковой | прямобоч | эвольвент | ||||||
| 1,8 | 1,5 | 1,4 | 1,45 | 2,25 | 1,43 | 1,8 | 1,35 | ||
| 2,0 | 1,55 | 1,7 | 1,6 | 2,5 | 1,49 | 2,2 | 1,7 | ||
| 2,2 | 1,7 | 2,05 | 1,7 | 2,65 | 1,55 | 2,45 | 2,1 | ||
| 2,65 | 1,9 | 2,4 | 1,75 | 2,8 | 1,6 | 2,9 | 2,35 | ||
Таблица 6.6 – Отношения Ks / Kds и Kt / Kdt для посадок с натягом [1, c.171]
| Диаметр вала d, мм | Ks / Kds при sВ, МПа | Kt / Kdt при sВ, МПа | ||||||
| 2,6 | 3,3 | 4,0 | 5,1 | 1,5 | 2,0 | 2,4 | 3,05 | |
| 2,75 | 3,5 | 4,3 | 5,4 | 1,65 | 2,1 | 2,6 | 3,25 | |
| 2,9 | 3,7 | 4,5 | 5,7 | 1,75 | 2,2 | 2,7 | 3,4 | |
| 3,0 | 3,85 | 4,7 | 5,95 | 1,8 | 2,3 | 2,8 | 3,55 | |
| 3,1 | 4,0 | 4,85 | 6,15 | 1,85 | 2,4 | 2,9 | 3,7 | |
| 3,2 | 4,1 | 4,95 | 6,3 | 1,9 | 2,45 | 3,0 | 3,8 | |
| 3,3 | 4,2 | 5,1 | 6,45 | 1,95 | 2,5 | 3,05 | 3,9 | |
| 3,35 | 4,3 | 5,2 | 6,6 | 2,0 | 2,55 | 3,1 | 3,95 | |
| Примечание. При установке с натягом колец подшипников табличные значения следует умножить на 0,9. |
При действии в одном сечении нескольких источников концентрации напряжений (например, посадка с натягом колеса и шпоночный паз) учитывают только наиболее опасный из них (с наибольшим значением KsD или KtD по формулам (6.17)).
6.3.2 Пример расчета вала на сопротивление усталости
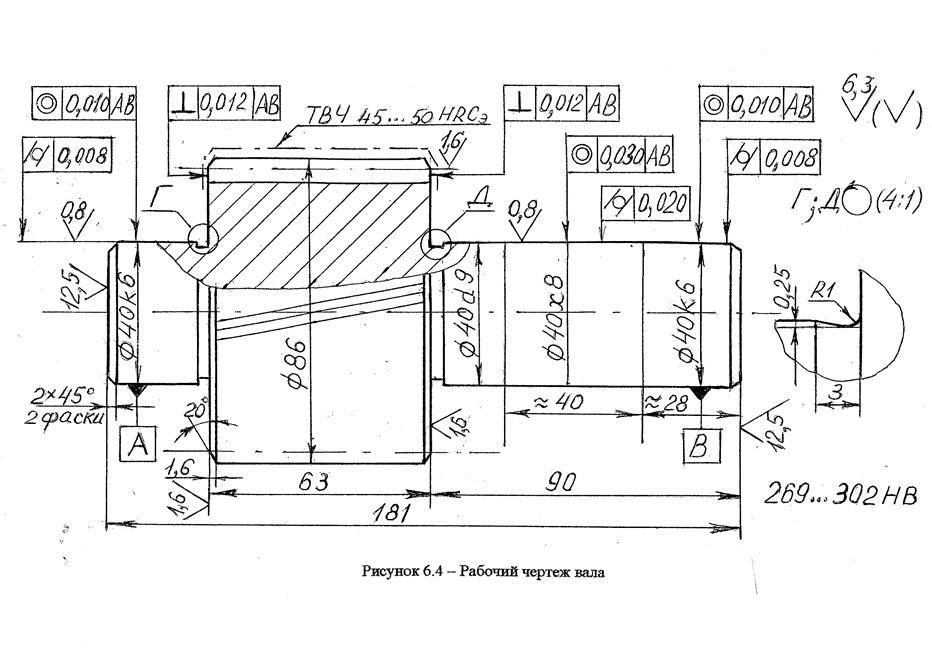
На рисунке 6.4 представлен рабочий чертеж вала, взятого в качестве примера в данной работе.
В соответствии с рисунком 6.1 и проверочным расчетом (п.6.2.2) наиболее опасными сечениями вала являются сечение 2 – посадка Æ40 Н8 / x8 колеса z2Б и сечение по галтели (обозначим его сечение 3) перехода вала в шестерню z1Т (проточка на рисунке 6.4).
Нагрузка вала : Т = 209 Н×м; изгибающие моменты: в сечении 2 М2 = 111 Н×м, в сечении 3 М3 = 200 Н×м (принято приближенно с запасом – по моменту на шестерне z1Т).
Механические характеристики стали 40Х (таблица 1.1) при диаметре заготовки < 120 мм :
|
sВ = 900 МПа, sТ = 750 МПа, tТ = 450 МПа, s–1 = 410 МПа, t–1 = 240 МПа, yt = 0,1.
Напряжения по формулам (6.15), где цифра у s и t обозначает номер сечения: sИ2 =
= 103×111/ (6,28×103) = 17,7 МПа, tК2 =103×209/(12,56×103) = 16,6 МПа; sИ3 = 103×200 /
/ (6,28×103) = 31,8 МПа, tК3 = tК2 =16,6 МПа.
Эффективные коэффициенты концентрации напряжений :
– сечение 2 – по таблице 6.6 для посадки с натягом при d = 40 мм и sВ = 900 МПа Ks / Kds= 4,3, Kt / Kdt = 2,6;
– сечение 3 – в соответствии с рисунком 6.2 t = (d1 – d) / 2 = (80 - 40) / 2 = 20 мм, галтель проточки для выхода шлифовального круга r = 1 мм, t / r = 20. Таблица 6.4 ограничена значениями t / r = 5, поэтому воспользуемся графиками [9, c.555], где при d1 / d = 80 / 40 = 2 и r / d = 0,025 Ks = 3,8, Kt = 2,5. По таблице 6.1 для легированной стали Kds =
= Kdt = 0,73. Тогда Ks / Kds = 3,8/ 0,73 = 5,21, Kt / Kdt = 2,5 / 0,73 = 3,42.
Коэффициенты KFs = 0,91 и KFt = 0,95 (таблица 6.2) для чистового шлифования при Ra = 0,8 мкм. По таблице 6.3 КV = 1 (без упрочнения поверхностей в рассматриваемых сечениях).
Коэффициенты снижения пределов выносливости по формулам (6.17) :
| Сечение 2 KsD = (4,3 + 1 / 0,91 – 1) / 1 = 4,4; KtD = (2,6 + 1 / 0,95 – 1) / 1 = 2,65; | Сечение 3 KsD = (5,21 + 1 / 0,91 – 1) / 1 = 5,31; KtD = (3,42 + 1 / 0,95 – 1) / 1 = 3,47. |
Пределы выносливости по формулам (6.16)
| s–1D = 410 / 4,4 = 93,2 МПа; | s–1D = 410 / 5,31 = 77,2 МПа; |
| t–1D = 240 ./ 2,65 = 98 МПа; | t–1D = 240 ./ 3,47 = 69,2 МПа. |
Коэффициенты запаса прочности по формулам (6.14) :
| Ss = 93,2 / 17,7 = 5,27; St = 2×98 / [16,6×(1 + 0,038)] = 11,37, где ytD = yt/ KtD = 0,1 / 2,65 = 0,038; | Ss = 77,2 / 31,8 = 2,43; St = 2×69,2 / [16,6×(1 + 0,029)] = 8,1, где ytD = 0,1 / 3,47 = 0,029 . |
Общий коэффициент запаса по формуле (6.12) :
| S = 5,27×11,37 / (5,272+11,372)1/2 = 4,78; S > [S] = 1,5...2,5 | S = 2,43×8,1 / (2,432+8,12)1/2 = 2,32; S » [S] = 1,5...2,5. |
Следовательно, сопротивление усталости в опасных сечениях вала при циклических напряжениях обеспечивается.
6.4 Прогиб вала–червяка
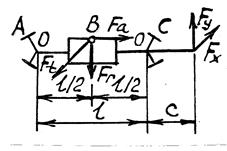
6.4.1 Червяк (рисунок 6.5) располагается симметрично относительно
| опор А и С и нагружен силами в зацеплении В (Ft, Fr, Fa) и на входном конце вала проек-циями (FX, FY) консольной силы. Согласно [2, c.332] и [3, c.261] прогибы y, мм, в точке В от сил : – окружной Ft y(Ft) = Ftl3 / (48EI) ; – радиальной Fr y(Fr) = Frl3 / (48EI) ; – осевой Fa y(Fa) = 0 – при симметрич-ном расположении червяка относительно опор |
Рисунок 6.5 – Cхема вала–червяка
|
– консольных FX, FY : y(FX, FY) = (FX, FY)сl2 / (16EI).
Суммарные прогибы по плоскостям X и Y ;
yX = y(Ft) + y(FX) = (3FXc + Ft l)l2 / (48EI);
yY = y(Fr) + y(FY) = (3FYc + Fr l)l2 / (48EI).
Общий прогиб в точке В червяка : yS = (yX2 + yY2)1/2 £ [y],
где ]y] = 0,005m – допускаемый прогиб червяка, мм (m – модуль, мм).
В приведенных здесь формулах EI – изгибная жесткость вала, Н×мм2; для стали Е = 2,1×105 МПа; для сплошного вала I = pd4 / 64, мм4.
В приближенных расчетах условно принимают d вала равным df1 – диаметру впадин червяка (в запас прочности).
6.4.2 Пример расчета прогиба вала–червяка
Исходные данные в соответствии с рнсунком 6.5 :
d = df1= 35 мм, l = 170 мм, с = 70 мм; Ft = 615 Н, Fr = 1336 Н, Fа = 3670 Н, сила муфты FМ =
= FХ = 125 Н. FY = 0; модуль червяка m = 6,3 мм.
Изгибная жесткость в сечении В : EI = 2,1×105×p×354/ 64 = 154,7×108 мм4
Прогибы в сечении В :
yX = (3×125×70 + 615×170)×1702 / (48×154,7×108) = 0,0051 мм;
yY = (1336×1703 / (48×154,7×108) = 0,009 мм;
yS = (0,00512 + 0,0092)1/2 = 0,0103 мм < [y] = 0,005×6,3 = 0,0315 мм.
Жесткость червяка при заданных силах обеспечивается.
Статические нагрузки двухконцевых лебедок
Одноконцевые лебедки в отличие от двухконцевых являются неуравновешенными механизмами. При подъеме такой механизм кроме полезного груза поднимает канаты, грузозахватывающее устройство, при отпускании в дополнение к грузу он тормозит и т.д., т.е. совершается лишняя работа, механизм дополнительно потребляет эл.энергию, увеличивается мощность Р эл.оборудования и эксплуатационные затраты.
Если число уравнений больше 2 (лифты), то вместо 2ой кабины навешивается балансировочный контргруз (противовес) – Gпр:
Gпр = G0 + α Gп (1) , где α – коэффициент уравновешивания.
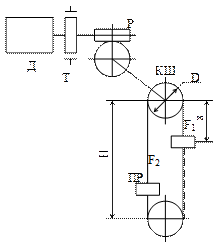В качестве примера рассмотрим лифтовую лебедку с червячным редуктором и канатоведущим шкивом.
Д – двигатель
Т – тормоз
Р – редуктор
КШ – канатоведущий шкив
ПР – противовес
К – кабина
│| – уравновешивающие канаты
Результат усилия на канатоведущем шкиве определяется разностью натяжений подвесных канатов: F = F1 – F2 (2)
С учетом сил трения F’тр и F’’тр в направлениях кабины и противовеса, а также веса канатов с весом погонного тетрад соотношение (2) будет
F = G+G0 +gкх –G0 – αGп – (H–х)gк ± (F’тр –F’’тр),
«+» – подъем, «–» – спуск F = G + gк(2х – H) ± Fтр2 – αGп (3)
Из (3) следует, что усилие на валу шкива будет состоять из усилий, обусловленных весом груза (активных) и силой трения (реактивной).
На валу двигателя эти силы будут составлять момент
Мс = [G + gк(2х – H) – αGп] D / (2ip) ± Мгр (4)
Из (4) видно, что Мс зависит от α и от высоты подъема Н и загрузки кабины G. Если Н невелико или используется уравновешивающие канаты, то составляющей gк(2х – H) пренебрегаем
Мс = (G – αGп) D / (2ip) ± Мгр (5)
Рассмотрим реакции опор двухконцевых лебедок
1. Подъем номинального груза (G = Gн)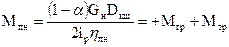 
(6)
2. Подъем пустой кабины (G = 0)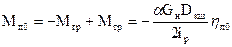 
(7)
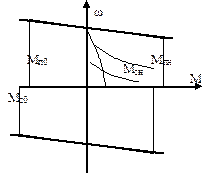3. Спуск (G = Gн) 
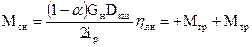(8)
4. Спуск (G = 0) (двигательный режим)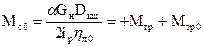 
(9)
Влияние коэффициента уравновешивания α на требуемую мощность оценим с помощью момента среднеквадратического. Зададимся циклом работы, когда лебедка поднимает номинальный груз за время tп àGн ; tс àG0. Считаем, время спуска равно подъему.
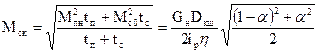(10)
При выводе считаем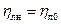 
, Мск = f (α)
Для нахождения минимума найдем производную dМск/dα = 0, решение αопт = 0,5.
Мск (α=0) / Мск (α=0) = 
Нагрузки – симметричны относительно начала координат.
Дата добавления: 2015-03-20; просмотров: 1189;