Системы связей каркаса производственного здания
Энергия 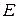 тела (без учета потенциальной энергии во внешнем силовом поле) связана с его массой
тела (без учета потенциальной энергии во внешнем силовом поле) связана с его массой 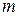
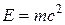 , (77)
, (77)
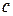 - скорость света в вакууме.
- скорость света в вакууме.
Энергия покоя тела
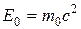 ,
,
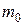 - масса покоящегося тела.
- масса покоящегося тела.
Кинетическая энергия релятивистской частицы
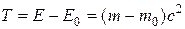 .
.
8. Связь между энергией 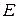 и импульсом
и импульсом 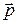 частицы.
частицы.
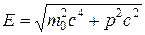 . (78)
. (78)
Образец теста по разделу «Механика»
1. Материальная точка движется по окружности радиусом 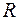 = 5 м так, что пройденный ею путь меняется со временем как
= 5 м так, что пройденный ею путь меняется со временем как 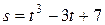 м. Определить величину ускорения
м. Определить величину ускорения 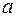 точки в момент
точки в момент 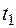 = 2 с. В произвольной точке траектории показать направления тангенциального, нормального и полного ускорения материальной точки.
= 2 с. В произвольной точке траектории показать направления тангенциального, нормального и полного ускорения материальной точки.
(Ответ: ≈ 20 м/с2 )
2. Диск вращается равнозамедленно в направлении, показанном на рисунке. Определить номер линии, по которой направлен вектор углового ускорения 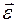 .
.
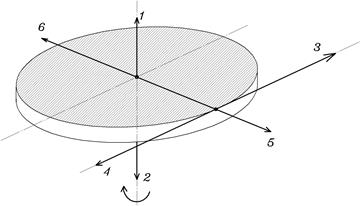 (Ответ: 1)
(Ответ: 1)
3. В каком случае скорость 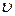 тела можно вычислить по формуле
тела можно вычислить по формуле 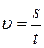 ? Указать номер правильного ответа.
? Указать номер правильного ответа.
1: 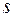 =6
=6 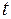 м 2:
м 2: 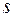 =6
=6 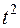 м 3:
м 3: 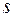 =(6
=(6 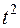 +
+ 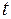 ) м 4:
) м 4: 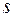 =(6
=(6 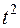 +1) м
+1) м
(Ответ: 1)
4. Тело массой 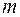 = 2 кг падает вертикально вниз с ускорением
= 2 кг падает вертикально вниз с ускорением 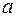 =9 м/с2 . Определить среднюю силу сопротивления воздуха.
=9 м/с2 . Определить среднюю силу сопротивления воздуха.
(Ответ: 2 Н)
5. Четыре шарика массами 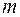 , 2
, 2 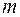 , 3
, 3 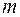 , 4
, 4 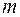 закреплены на невесомом стержне на одинаковом расстоянии
закреплены на невесомом стержне на одинаковом расстоянии 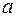 = 0,1 м друг от друга. На каком расстоянии от крайнего левого шарика находится центр масс системы?
= 0,1 м друг от друга. На каком расстоянии от крайнего левого шарика находится центр масс системы?
(Ответ: 20 см)
6. Четыре шарика одинаковой массы 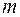 = 50 г закреплены невесомыми стержнями в вершинах квадрата со стороной
= 50 г закреплены невесомыми стержнями в вершинах квадрата со стороной 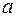 = 10 см. Определить момент инерции
= 10 см. Определить момент инерции 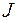 системы относительно оси
системы относительно оси 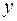 . Шарики рассматривать как материальные точки.
. Шарики рассматривать как материальные точки.

(Ответ: 0,001 кг· м2)
7. Чтобы закатить барабан радиуса 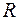 = 1 м на ступеньку высотой
= 1 м на ступеньку высотой 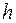 = 50 см, к нему прикладывают горизонтальную силу
= 50 см, к нему прикладывают горизонтальную силу 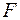 = 2 Н. Определить величину момента
= 2 Н. Определить величину момента 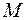 этой силы относительно точки О.
этой силы относительно точки О.
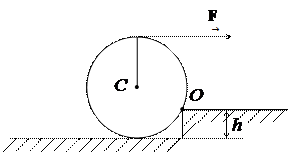 |
(Ответ: 3 Н· м)
8. С какой угловой скоростью 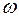 должен вращаться диск радиуса
должен вращаться диск радиуса 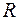 = 0,8 м и массой
= 0,8 м и массой 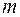 = 0,5 кг, чтобы его кинетическая энергия
= 0,5 кг, чтобы его кинетическая энергия 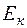 составляла 2 Дж?
составляла 2 Дж?
(Ответ: 5 рад/c)
9. Стержень длиной 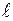 = 1 м ставят вертикально на конец
= 1 м ставят вертикально на конец  и отпускают. Стержень падает без проскальзывания, вращаясь вокруг точки
и отпускают. Стержень падает без проскальзывания, вращаясь вокруг точки  . Определить угловое ускорение
. Определить угловое ускорение 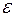 стержня в момент, когда он составляет угол
стержня в момент, когда он составляет угол 
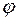 = 60° с плоскостью.
= 60° с плоскостью. 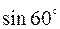
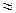 0,9;
0,9; 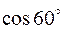 =0,5.
=0,5.
 |
(Ответ: 7,5 рад/с2)
 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Тема «Кинематика»
Пример 1.Частица движется по окружности радиусом 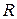 = 50 см так, что зависимость ее пути
= 50 см так, что зависимость ее пути 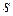 от времени
от времени 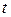 имеет вид
имеет вид 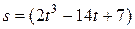 м. Определить скорость
м. Определить скорость 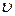 и ускорение
и ускорение 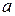 частицы в момент
частицы в момент 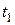 =2 с. Найти угол
=2 с. Найти угол 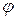 между скоростью и ускорением частицы в заданный момент времени.
между скоростью и ускорением частицы в заданный момент времени.
Дано: 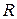 =0,5 м,
=0,5 м, 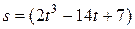 м ,
м , 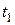 =2 с. Найти:
=2 с. Найти: 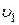 ,
, 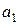 ,
, 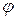 .
.
Решение. Скорость представляет собой производную от пути по времени
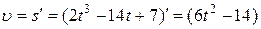 м/c .
м/c .
В момент 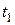 =2 с,
=2 с,
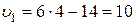 м/c .
м/c .
Тангенциальное ускорение
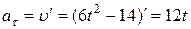 м/c2,
м/c2, 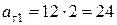 м/c2 .
м/c2 .
Нормальное ускорение
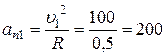 м/c2.
м/c2.
Полное ускорение 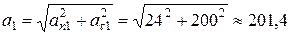 м/c2 .
м/c2 .
Скорость  и
и  направлены по касательной к окружности,
направлены по касательной к окружности, 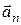 - к ее центру (рис.10).
- к ее центру (рис.10).
Рисунок 10 –Направления скорости и ускорения.
 ;
;  .
.
Ответ: 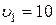 м/c ,
м/c , 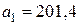 м/c2 ,
м/c2 , 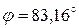 .
.
Пример 2. Цилиндр радиусом 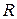 катится без скольжения со скоростью
катится без скольжения со скоростью 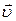 (рис.11). Определить скорости точек А и В, а также радиусы кривизны их траекторий.
(рис.11). Определить скорости точек А и В, а также радиусы кривизны их траекторий.
Дано: 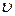 ,
,  . Найти:
. Найти: 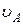 ,
, 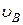 ,
, 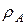 ,
, 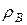 .
.
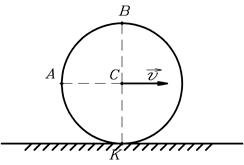
Рис. 11.
Решение.
1). Качение цилиндра можно представить как сумму двух движений: поступательного с постоянной скоростью 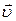 (рис.12,
(рис.12, 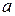 ) и вращательного вокруг центра масс
) и вращательного вокруг центра масс 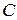 (рис.12,
(рис.12, 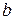 ).
).
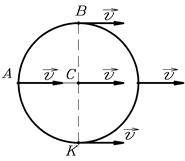
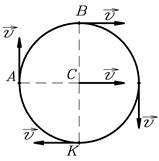
Рис.12,  . Рис.12,
. Рис.12,  .
.
Т.к. скорость точки К касания цилиндра с землей равна нулю, то значит, при вращении точки обода цилиндра движутся также со скоростью 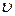 . В результате сложения скоростей при поступательном и вращательном движениях находим скорости точек
. В результате сложения скоростей при поступательном и вращательном движениях находим скорости точек 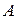 и
и 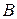
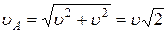 ;
; 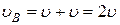 .
.
Направления векторов  и
и  показаны на рисунке 13.
показаны на рисунке 13.
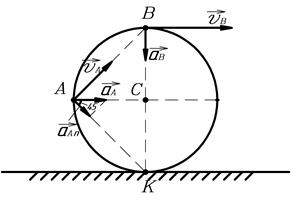
Рис.13.
2). Ускорение точек  и
и  обусловлено вращением цилиндра,
обусловлено вращением цилиндра,
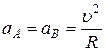 .
.
Векторы 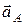 и
и 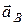 направлены к центру
направлены к центру  цилиндра. Нормальное ускорение точки
цилиндра. Нормальное ускорение точки  перпендикулярно скорости
перпендикулярно скорости 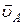 (рис.13),
(рис.13),
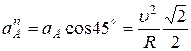 .
.
Нормальное ускорение точки 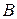 равно ее полному ускорению
равно ее полному ускорению
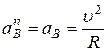 .
.
Т.к. радиус кривизны траектории 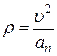 , то
, то
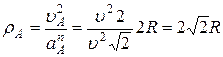 ,
,
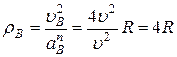 .
.
Ответ: 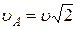 ,
, 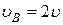 .
. 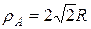 ,
, 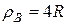 .
.
Тема «Законы Ньютона»
Пример 3. Тело скользит по наклонной плоскости, составляющей угол 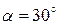 с горизонтом. Пройденный телом путь
с горизонтом. Пройденный телом путь 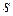 меняется со временем
меняется со временем 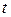 по уравнению
по уравнению 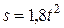 м. Определить коэффициент трения
м. Определить коэффициент трения 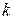 тела о плоскость.
тела о плоскость.
Дано: 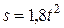 м,
м, 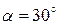 . Найти:
. Найти: 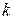 ..
..
Решение. Скорость тела равна
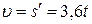 м/c.
м/c.
Ускорение тела
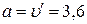 м/c2.
м/c2.
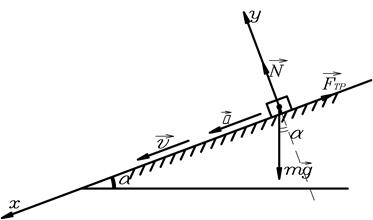
Рис.14.
При движении на тело действуют сила тяжести 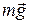 , сила трения
, сила трения 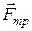 , сила реакции опоры
, сила реакции опоры  (рис.14).
(рис.14).
Запишем 2-ой закон Ньютона 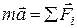 в проекциях на оси x и y :
в проекциях на оси x и y :
(x) 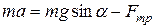 , (1)
, (1)
(y) 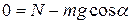 . (2)
. (2)
Из (1): 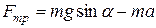 ,
,
из (2): 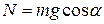 .
.
Т.к. 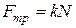 , то коэффициент трения
, то коэффициент трения
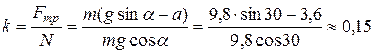 .
.
Ответ: 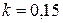 .
.
Пример 4. Сфера радиусом 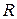 =1 м равномерно вращается вокруг вертикального диаметра с частотой 36 мин-1. Внутри сферы находится шарик массой
=1 м равномерно вращается вокруг вертикального диаметра с частотой 36 мин-1. Внутри сферы находится шарик массой 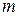 =50 г. Найти, на какой высоте, отсчитываемой от нижней точки сферы, шарик займет положение равновесия относительно сферы. Определить силу давления шарика на сферу в этом положении.
=50 г. Найти, на какой высоте, отсчитываемой от нижней точки сферы, шарик займет положение равновесия относительно сферы. Определить силу давления шарика на сферу в этом положении.
Дано: 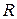 =1 м,
=1 м, 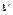 =36 мин-1=0,6 с-1,
=36 мин-1=0,6 с-1, 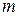 =0,05 кг. Найти:
=0,05 кг. Найти: 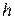 ,
, 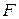 .
.
Решение: На шарик действуют сила тяжести 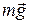 и реакция опоры
и реакция опоры  (рис.15).
(рис.15).
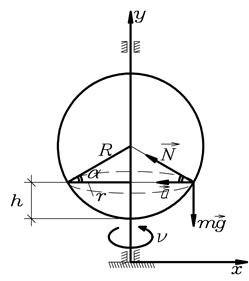
Рис.15.
Т.к. вращение равномерное, то тангенциальное ускорение шарика
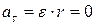 .
.
Полное ускорение шарика равно нормальному,
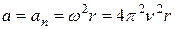 ,
,
и направлено к центру его траектории. Т.к. радиус траектории 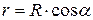 , то
, то
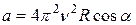 . (1)
. (1)
Запишем 2-ой закон Ньютона для шарика в проекции на оси x и y
(x) 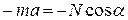 , (2)
, (2)
(y) 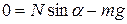 . (3)
. (3)
Отсюда 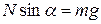 и
и 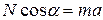 . Поделим два последних уравнения одно на другое,
. Поделим два последних уравнения одно на другое,
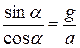 .
.
Подставим из (1) выражение для ускорения
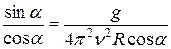 .
.
Отсюда 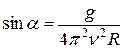 .
.
Т.к. 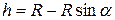 , то
, то
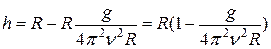 .
.
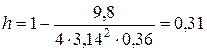 м =
м = 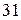 см.
см.
Из (3) найдем, что 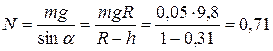 Н.
Н.
Сила давления шарика на сферу численно равна силе реакции опоры, 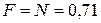 Н.
Н.
Ответ: 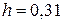 м ;
м ; 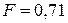 Н.
Н.
Тема «Импульс тела. Центр масс»
Пример 5. Шарик массой 50 г, движущийся со скоростью 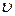 =2 м/с под углом
=2 м/с под углом 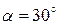 к стенке, абсолютно упруго соударяется с ней. Продолжительность удара
к стенке, абсолютно упруго соударяется с ней. Продолжительность удара 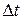 =0,01 с. Определить среднюю силу, действующую на стенку во время удара.
=0,01 с. Определить среднюю силу, действующую на стенку во время удара.
Дано: 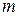 =0,05 кг,
=0,05 кг, 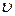 =2 м/c,
=2 м/c, 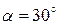 ,
, 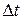 =0,01 c. Найти:
=0,01 c. Найти:  .
.
Решение. Изменение количества движения (импульса) шарика равно сумме импульсов действующих на него сил:
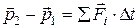 . (1)
. (1)
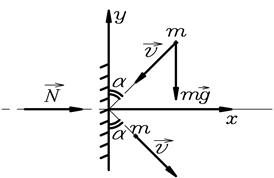
Рис.16.
На шарик действуют сила тяжести 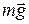 и, во время удара, сила реакции стенки
и, во время удара, сила реакции стенки  (рис.16).
(рис.16).
Спроецируем уравнение (1) на ось x:
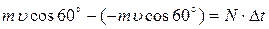 .
.
Отсюда
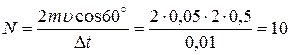 Н.
Н.
Т.к. сила, действующая на стенку, численно равна силе реакции опоры, то
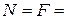 10 Н.
10 Н.
Ответ: 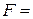 10 Н.
10 Н.
Пример 6. Четыре точечные массы 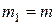 ,
, 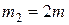 ,
, 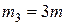 и
и 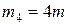 находятся в вершинах квадрата со стороной
находятся в вершинах квадрата со стороной 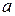 (рис.17). Определить положение центра масс данной системы.
(рис.17). Определить положение центра масс данной системы.
Дано: 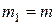 ,
, 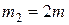 ,
, 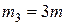 ,
, 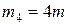 ,
, 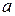 . Найти:
. Найти: 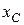 -?
-? 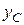 -?
-?
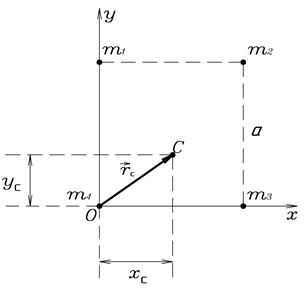
Рис.17.
Решение. Расположим начало координатных осей x и y в точке  . Тогда координаты центра масс
. Тогда координаты центра масс 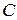 равны
равны
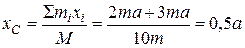 ,
,
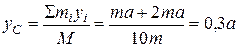 .
.
Величина радиус-вектора центра масс
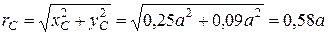 .
.
Ответ: 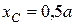 ,
, 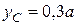 .
.
Тема «Динамика вращательного движения»
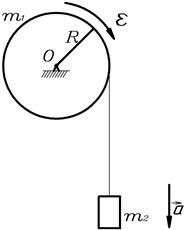
Пример 7. На барабан массой 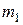 =3 кг намотан шнур, к концу которого привязан груз массой
=3 кг намотан шнур, к концу которого привязан груз массой 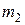 =2 кг (рис.18). Найти ускорение
=2 кг (рис.18). Найти ускорение 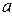 груза и силу натяжения
груза и силу натяжения 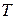 шнура, считая барабан однородным диском. Трением пренебречь.
шнура, считая барабан однородным диском. Трением пренебречь.
 Дано:
Дано: 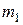 =3 кг,
=3 кг, 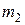 =2 кг,
=2 кг,
барабан – диск. Найти: 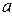 ,
, 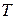 .
.
Решение. На груз действуют
сила тяжести 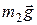 и сила
и сила
натяжения шнура 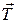 (рис.19) .
(рис.19) .
Т.к. груз совершает
поступательное движение,
запишем для него 2-ой закон Ньютона Рис.18
в проекции на ось y, направленную
вертикально вниз, Рис.18.
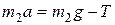 . (1)
. (1)
На барабан действуют сила натяжения 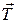 , сила тяжести
, сила тяжести 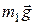 и реакция опоры
и реакция опоры  (рис.20).
(рис.20).
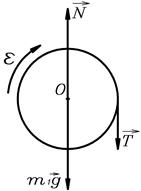
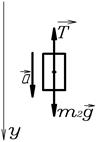
Рис.19. Рис.20.
Т.к. барабан вращается, воспользуемся основным законом динамики вращательного движения 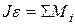 и запишем его относительно оси вращения, проходящей через точку
и запишем его относительно оси вращения, проходящей через точку 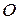 :
:
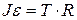 , (2)
, (2)
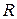 - радиус барабана. Моменты сил
- радиус барабана. Моменты сил  и
и 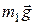 относительно точки
относительно точки 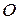 равны нулю.
равны нулю.
Т. к. барабан – однородный диск, его момент инерции
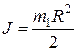 .
.
Угловое ускорение барабана 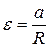 . Подставив
. Подставив 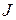 и
и 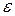 в уравнение (2), получаем
в уравнение (2), получаем
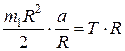 . (3)
. (3)
Отсюда 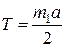 . (4)
. (4)
Подставим 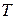 в (1):
в (1):
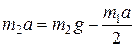 .
.
Тогда 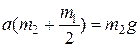 .
.
Отсюда ускорение
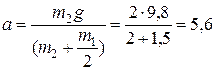 м/с2.
м/с2.
Сила натяжения шнура из уравнения (4):
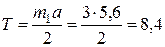 Н.
Н.
Ответ:  м/c2 ,
м/c2 , 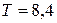 Н.
Н.
Пример 8. Лестница массой 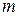 =16 кг приставлена к вертикальной стене под углом 20° к ее поверхности. На лестнице на расстоянии
=16 кг приставлена к вертикальной стене под углом 20° к ее поверхности. На лестнице на расстоянии 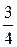 ее длины , от нижнего конца, стоит человек массой
ее длины , от нижнего конца, стоит человек массой 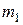 =75 кг. Каким должен быть коэффициент трения между основанием лестницы и поверхностью пола, чтобы лестница не соскользнула? Трением между лестницей и стенкой пренебречь.
=75 кг. Каким должен быть коэффициент трения между основанием лестницы и поверхностью пола, чтобы лестница не соскользнула? Трением между лестницей и стенкой пренебречь.
Дано: 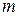 =16 кг,
=16 кг, 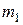 =75 кг,
=75 кг, 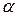 =20°,
=20°, 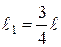 . Найти:
. Найти: 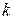 .
.
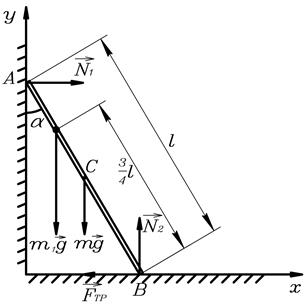
Рис.21.
Решение. Обозначим 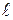 - длина лестницы. На лестницу с человеком действуют сила тяжести лестницы
- длина лестницы. На лестницу с человеком действуют сила тяжести лестницы 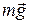 , человека
, человека 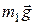 , сила трения
, сила трения 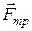 и реакции опор
и реакции опор 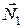 и
и 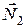 (рис.21).
(рис.21).
Т.к. система находится в равновесии, то сумма действующих на нее сил и моментов сил должна быть равна нулю.
Запишем условие равенства нулю суммы сил в проекции на ось y:
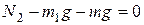 .
.
Отсюда 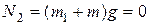 .
.
Запишем условие равенства нулю моментов сил, относительно точки 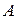 :
:
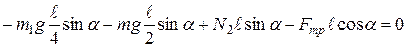 .
.
Сокращая на  и учитывая, что
и учитывая, что 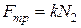 , получаем
, получаем
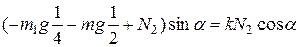 .
.
Отсюда 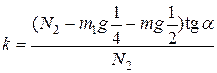 =
= 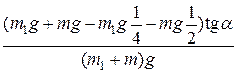 =
=
= 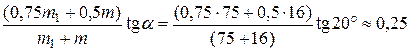
Ответ: 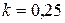 .
.
Тема «Работа. Механическая энергия»
Пример 9. Тонкий стержень длиной 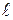 =0,8 м может свободно вращаться вокруг вертикальной оси, проходящей его верхний конец. Стержень отклонили на угол
=0,8 м может свободно вращаться вокруг вертикальной оси, проходящей его верхний конец. Стержень отклонили на угол 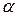 =60 ° и отпустили (рис.22). Определить угловую скорость
=60 ° и отпустили (рис.22). Определить угловую скорость  стержня, линейную скорость его нижнего конца и скорость центра масс
стержня, линейную скорость его нижнего конца и скорость центра масс  в момент прохождения стержнем положения равновесия.
в момент прохождения стержнем положения равновесия.
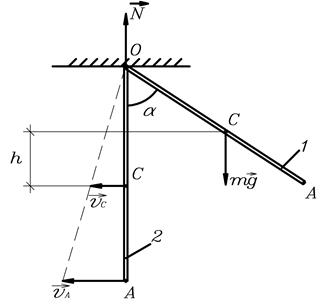
Рис.22.
Дано: 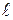 =0,8 м,
=0,8 м, 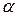 =60 °. Найти:
=60 °. Найти: 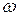 ,
, 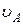 ,
, 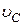 .
.
Решение.
Изменение кинетической энергии стержня равно работе сил, приложенных к нему:
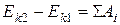 (1)
(1)
(теорема о кинетической энергии).
В начальный момент стержень неподвижен, 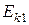 =0.
=0.
В момент прохождения положения равновесия 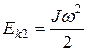 ,
,
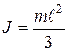 - момент инерции однородного стержня относительно оси вращения, проходящей через точку подвеса
- момент инерции однородного стержня относительно оси вращения, проходящей через точку подвеса 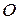 . Тогда
. Тогда
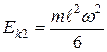 . (2)
. (2)
На стержень действуют сила тяжести 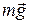 и реакция опоры
и реакция опоры  . Сила
. Сила  не совершает работы, т.к. точка ее приложения неподвижна. Работа силы тяжести
не совершает работы, т.к. точка ее приложения неподвижна. Работа силы тяжести
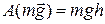 .
.
Т.к. 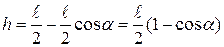 , то
, то
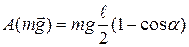 . (3)
. (3)
Подставляя в (1) уравнения (2) и (3), получаем
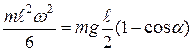 .
.
Отсюда 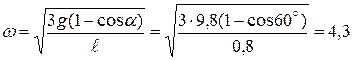
 .
.
Скорость точки  ,
, 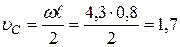 м/с.
м/с.
Скорость точки  ,
, 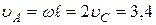 м/с.
м/с.
Ответ: 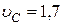 м/с,
м/с, 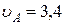 м/с.
м/с.
Пример 10. Шар, движущийся со скоростью 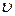 =4 м/с, закатывается на наклонную плоскость, составляющую угол
=4 м/с, закатывается на наклонную плоскость, составляющую угол 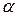 = 30° с горизонтом (рис.23). Какое расстояние
= 30° с горизонтом (рис.23). Какое расстояние 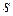 пройдет шар по наклонной плоскости за счет его кинетической энергии? Трением пренебречь.
пройдет шар по наклонной плоскости за счет его кинетической энергии? Трением пренебречь.
Дано: 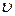 =4 м/с,
=4 м/с, 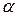 = 30° . Найти:
= 30° . Найти: 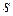 .
.
Решение. Применим теорему о кинетической энергии:
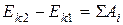 . (1)
. (1)
В конце движения шар останавливается, поэтому 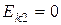 .
.
Начальная кинетическая энергия шара
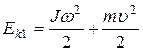 , (2)
, (2)
т.к. движение шара складывается из поступательного и вращательного. В формуле (2) 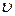 - скорость центра масс
- скорость центра масс 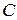 шара (рис.23).
шара (рис.23).
Момент инерции шара 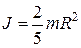 , его угловая скорость
, его угловая скорость 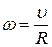 .
.
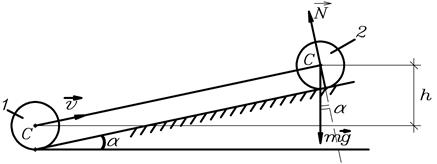
Рис.23.
Тогда 
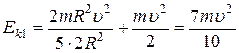 (3)
(3)
Сила реакции опоры  работы не совершает. Работа силы тяжести
работы не совершает. Работа силы тяжести
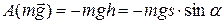 . (4)
. (4)
Подставляя выражения для 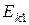 и
и 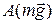 в (1), получаем
в (1), получаем
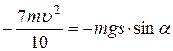 .
.
Отсюда 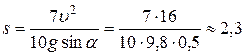 м.
м.
Ответ: 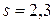 м.
м.
Тема «Уравнения гидродинамики»
Пример 11. Вода из трубы диаметром 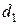 =5 см, расположенная на глубине 1 м, поступает в здание под давлением 3 атм со скоростью 0,5 м/с. На верхнем этаже на высоте 10 м труба сужается до диаметра
=5 см, расположенная на глубине 1 м, поступает в здание под давлением 3 атм со скоростью 0,5 м/с. На верхнем этаже на высоте 10 м труба сужается до диаметра 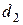 =2,5 см. Вычислить скорость течения и давление в трубе на верхнем этаже (вязкостью воды пренебречь).
=2,5 см. Вычислить скорость течения и давление в трубе на верхнем этаже (вязкостью воды пренебречь).
1 атм=101,3∙103 Па.
Дано: 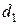 =5 см=5∙10-2 м,
=5 см=5∙10-2 м, 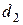 =2,5 см=2,5∙10-2 м,
=2,5 см=2,5∙10-2 м, 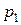 =3 атм=303,9∙103 Па,
=3 атм=303,9∙103 Па, 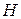 =1 м,
=1 м, 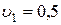 м/с,
м/с, 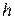 =10 м. Найти:
=10 м. Найти: 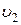 ,
, 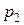 .
.
Решение. Из уравнения неразрывности вычислим скорость движения воды в узком сечении трубы
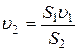 .
.
Т.к. площади сечений 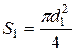 и
и 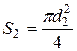 , то
, то
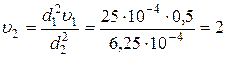 м/с .
м/с .
Уравнение Бернулли
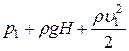 =
= 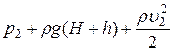 .
.
Отсюда
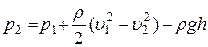 .
.
Подставим числовые данные, учитывая, что плотность воды 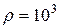 кг/м3 ,
кг/м3 , 
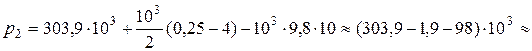
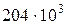 Па.
Па.
Ответ: 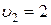 м/с ,
м/с , 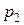 =204∙103 Па.
=204∙103 Па.
Пример 12. Для измерения скорости протекания газа используют трубку Вентури (трубку с сужением, в которую врезан жидкостный манометр, рис.24).
Определить скорость движения газа 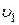 в широкой части трубки, если известны плотность
в широкой части трубки, если известны плотность 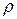 газа и плотность
газа и плотность 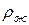 жидкости, площади
жидкости, площади 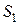 и
и 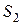 сечений трубки, разность уровней
сечений трубки, разность уровней 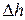 жидкости в манометре.
жидкости в манометре.
Дано: 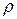 ,
, 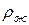 ,
, 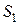 ,
, 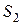 ,
, 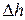 . Найти:
. Найти: 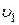 .
.
Решение. Т.к. трубка тока газа расположена горизонтально, то уравнение Бернулли для нее имеет вид
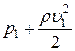 =
= 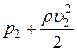 , (1)
, (1)
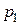 и
и 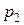 - статическое давление газа в широком сечении 1 и в узком сечении 2.
- статическое давление газа в широком сечении 1 и в узком сечении 2.
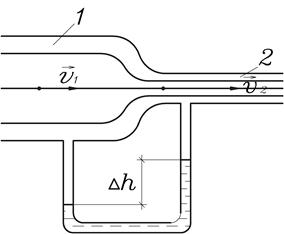
Рис.24.
Из (1):
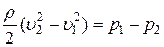 . (2)
. (2)
Разность статических давлений 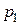 и
и 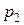 уравновешивается гидростатическим давлением столбика жидкости высотой
уравновешивается гидростатическим давлением столбика жидкости высотой 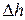
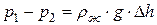 . (3)
. (3)
Из (2):
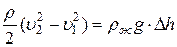 . (4)
. (4)
Скорости 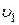 и
и 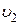 связаны уравнением неразрывности
связаны уравнением неразрывности
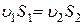 .
.
Отсюда 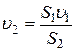 . Подставим
. Подставим 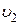 в (4):
в (4):
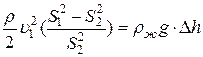 .
.
Получаем 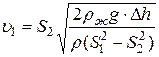 .
.
Ответ: 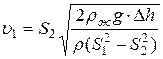 .
.
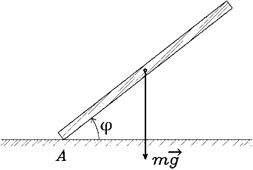
Системы связей каркаса производственного здания
Связи явл. основ. частью каркаса производ-го зд. и предназначены для: ─ обеспечения неизменяемости пространс-ой системы каркаса;
─ создания жесткости каркаса, необходимой для обеспечения нормальных условий эксплуатации здания;
─ восприятия ветровых и горизонтальных (продольных и поперечных) крановых воздействий, перераспределения и передачи их на фундаменты;
─ обеспечения проектного положения конструкций на стадии их монтажа.
Все связи произв-го зд. состоят из двух систем: связи между колоннами, связи по покрытию.
Связи по покрытию
Связи по покрытию обеспечивают общую пространственную жесткость каркаса зд., устойчивость некоторых сжатых элементов ферм (под фонарем) из плоскости. Кроме того, связи по покрытию необходимы для монтажа каркаса зд..
Система связей покрытия состоит из горизонтальных и вертикальных связей. Горизонтальные связи располагаются в плоскостях нижнего, верхнего поясов ферм и верхнего пояса фонаря. Горизонтальные связи состоят из поперечных и продольных (рис. 11.10 и 11.11).
Элементы верхнего пояса стропильных ферм сжаты, поэтому необходимо обеспечить их устойчивость из плоскости ферм. Ребра кровельных плит и прогоны могут рассматриваться как опоры, препятствующие смещению верхних узлов из плоскости фермы при условии, что они закреплены от продольных перемещений связями.
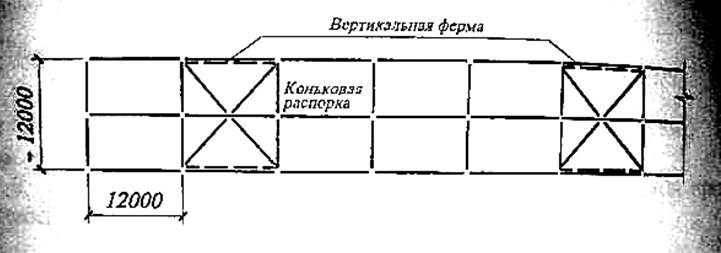
Для закрепления плит и прогонов от продольных смещений устраиваются поперечные связи по верхним поясам ферм, которые целесообразно располагать в торцах цеха с тем, чтобы они обеспечивали пространственную жесткость покрытия. При большой длине здания или температурного блока (более 144 м) устанавливаются дополнительные поперечные связевые фермы. Это уменьшает поперечные перемещения поясов ферм, возникающие вследствие податливости связей.Необходимо обращать особое внимание на завязку узлов ферм в пределах фонаря, где нет кровельного настила. Здесь для раскрепления узлов верхнего пояса ферм из их плоскости предусматриваются распорки, причем такие распорки в коньковом узле фермы обязательны. Распорки прикрепляются к торцовым связям в плоскости верхних поясов ферм. Связи по верхнему поясу фонаря (см. рис. 11.11) проектируются аналогично.
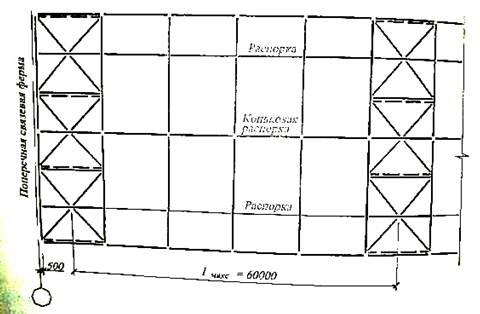
В однопролетных зданиях большой высоты (H0>18 м), в зданиях с мостовыми кранами грузоподъемностью Q.>10 т, с кранами тяжелого и весьма тяжелого режимов работы при любой грузоподъемности обязательна система связей по нижним поясам ферм. Связи обеспечивают совместную работу системы плоских рам, вследствие чего поперечные деформации каркаса от действия сосредоточенной силы значительно уменьшаются (рис. 11.12, а).
Поперечные связи закрепляют продольные, а в торцах здания они необходимы и для восприятия ветровой нагрузки, направленной на торец здания.
Для сокращения свободной длины растянутой части нижнего пояса приходится в некоторых случаях предусматривать растяжки, закрепляющие нижний пояс в боковом направлении.В длинных зданиях, состоящих из нескольких температурных блоков, поперечные связевые фермы по верхним и нижним поясам ставят у каждого температурного шва (как у троцов), имея в виду, что каждый температурный блок представляет собой законченный пространственный комплекс. Стропильные фермы обладают незначительной боковой жесткостью, а потому процесс монтажа без их предварительного взаимного раскрепления недопустим. Поэтому необходимо устраивать вертикальные связи между фермами, располагающиеся в плоскости вертикальных стоек стропильных ферм (см. рис. 11.10, в); для удобства крепления элементов связей эти стойки часто проектируют крестового сечения (из двух уголков). Обычно устраиваются одна-две вертикальные связи по ширине пролета (через 12—15 м).
.
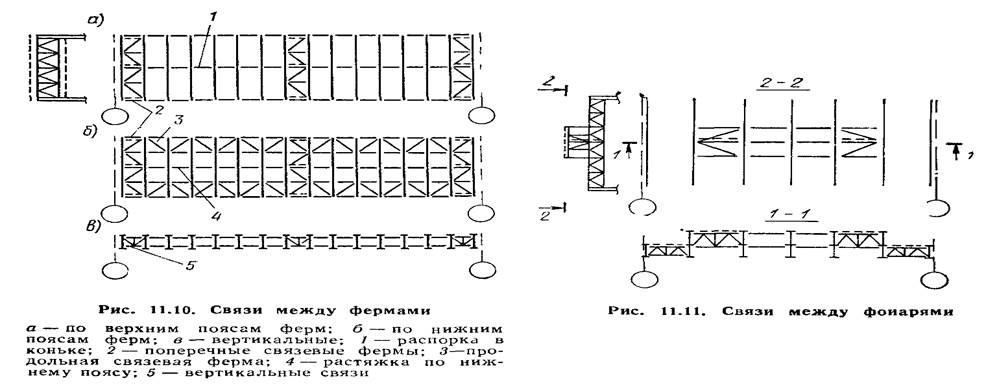
( из методы)Связи по покрытию располагают:
1) в плоскости верхних поясов стропильных ферм - поперечные связевые фермы и продольные элементы между верхними поясами стропильных ферм (распорки). Поперечные связевые фермы ставятся в крайних шагах температурного блока и в средней части покрытия протяженных температурных блоков, при этом расстояние (в осях) между поперечными связевыми фермами не должно превышать 60м. B коньковых узлах стропильных ферм должны быть установленьконьковые распорки
2) в плоскости нижних поясов стропильных ферм - поперечные и продольные связевые фермы и при необходимости продольные элементы между нижними поясами стропильных ферм (растяжки) (рис. 3.5). Поперечные связевые фермы по нижним поясам находятся в тех же осях, что и по верхним поясам. Продольные связевые фермы располагаются вдоль крайних рядов колонн, а в многопролетных зданиях - вдоль средних рядов колонн не реже чем через пролет при эксплуатации кранов групп режимов 6К-8К и через два пролета в прочих зданиях
3) в плоскости вертикальных стоек стропильных ферм в торцах и середине связевого блока - вертикальные связи между фермами. Они располагаются в тех же шагах, что и поперечные связевые фермы по нижним и верхним поясам стропильных ферм;
4) в плоскости верхних поясов фонарей и в вертикальной плоскости - связи по фонарям
При шаге 6 м применяют крестовую решетку, раскосы которой работают на растяжение (рис. 3.4). При шаге строп ферм 12м элементы связевой решетки получаются тяжелыми, поэтому доп устанавливается продольный элемент длиной 12м, кот поддерживает диагональные элементы в середине их пролета.
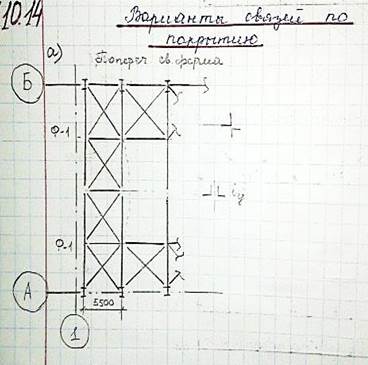


 горизонтальных связей по фонарю
горизонтальных связей по фонарю

По верхним
по нижним
компоновка поперечной рамы пром. зд.
Для компоновки необходимо знать технические характеристики мостового крана
Грузоподъемность 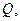 т
т
Главный крюк ; Вспомогательный крюк; Максимальное давление колеса  т. Вес тележ-ки
т. Вес тележ-ки 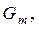 т. Вес крана с тележ-кой
т. Вес крана с тележ-кой 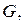 т . Тип кранового рельса . Режим работы крана
т . Тип кранового рельса . Режим работы крана
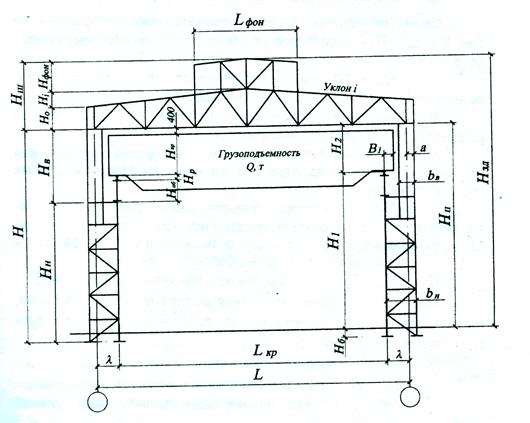
Схема поперечной рамы с обозначениями, где H1 - расстояние от поверхности пола (уровня земли) до отметки головки подкранового рельса;
Н2 = Нкр + 200 мм - расстояние от головки подкранового рельса до нижнего пояса стропильной фермы;
Нкр - высота мостового крана (габаритный размер, принимаемый по ГОСТ на мостовые краны) (прил. 5);
200+400 мм - зазор, который учитывает возможные прогибы стропильных ферм в пролете и отклонение габаритов мостовых кранов по высоте;
Hп= H1 + H2 - полезная высота цеха - расстояние от поверхности пола до нижнего пояса стропильной фермы, рекомендуется принимать кратным 0,6 м для возможности устройства стенового ограждения из типовых железобетонных панелей;
Нв = Нпб + Нр + Н2- высота надкрановой части колонны;
Нпб = 0,4 м- ориентировочная высота подкрановой балки, определяемая в зависимости от шага поперечных рам В, т.е. пролета подкрановой балки (В = Lпб)
Нр - высота кранового рельса;
Нн= Нп - Нв+Нб - высота подкрановой части колонны;
Нб = 0,6 -1,0 м- заглубление базы колонны ниже нулевой отметки уровня пола;
Н = Нв + Нн- высота колонны;
Н0 - высота стропильной фермы на опоре, принимается (по заданию) равной 3,15 м при уклоне верхнего пояса i = 1,5% либо 2,2 м при i= 1/8+1/12;
Нфон - высота фонаря, принимается равной 3,3 м при пролете цеха L = 24 м или 3,8 м при L = 30 и более метров;
Нш = Н0+ i * 0,5 * L + Нфон - высота шатровой части цеха (высота покрытия);
Нзд = Нп + Нш - высота цеха;
Ьв = 2 *а - ширина верхней (надкрановой) части колонны, из условий жесткости Ьв>(1/12) Нв
а - расстояние от кромки колонны до оси ("привязка" колонны), принимается равным 250 мм. При устройстве прохода в надкрановой части колонны размером 400 мм по ширине и 1800 мм по высоте (режим работы кранов 7К) принимается равным 500 мм;
вн = а + λ - ширина нижней (подкрановой) части колонны, из условий жесткости Bн>( 1/20) * Нн;
λ - расстояние между разбивочной осью колонны и осью подкрановой балки, принимается равным 750 мм для зданий, оборудованных мостовыми кранами грузоподъемностью Q < 50 т, и при отсутствии прохода в надкрановой части колонны. Последующие размеры λ кратны 250 мм;
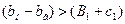 - условие, обеспечивающее прохождение мостового крана по подкрановым путям;
- условие, обеспечивающее прохождение мостового крана по подкрановым путям;
B1 - ширина выступающей части мостового крана
С1 - минимальный зазор, который устанавливается равным 60 мм для мостовых кранов грузоподъемностью Q < 50 т и 75 мм -для кранов большей грузоподъемности.
При невыполнении условия, обеспечивающего прохождение мостового крана по подкрановым путям, необходимо увеличить ширину подкрановой части колонны крайнего ряда bн на 250 мм. В случае устройства прохода шириной 400 мм вне надкрановой части колонны (режим работы кранов 7К) условие, обеспечивающее прохождение мостового крана по подкрановым путям, дополняется размером 450 мм: 400 мм предусмотрено на ширину прохода и 50 мм - на размер уголка ограждения:

L - пролет цеха;
LKp = L- 2 λ -пролет мостового крана;
Lфон -пролет фонаря; принимается 6м для L=24 , 12 для L=30,36м
Дата добавления: 2015-03-20; просмотров: 2455;
