Интерполяционная формула Ньютона
Получим еще одну форму записи интерполяционного многочлена, строящегося по набору узлов интерполяции 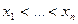 и значений функции
и значений функции 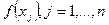 , в этих узлах. Пусть
, в этих узлах. Пусть 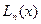 - отвечающий имеющемуся набору данных интерполяционный многочлен Лагранжа (180). Тогда справедливо равенство:
- отвечающий имеющемуся набору данных интерполяционный многочлен Лагранжа (180). Тогда справедливо равенство:
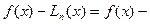
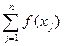
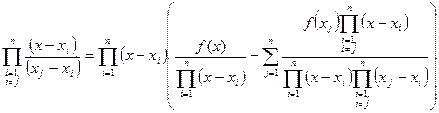 .
.
Учитывая, что 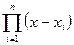 , стоящее в знаменателе последней дроби выражения в скобках, отличается от
, стоящее в знаменателе последней дроби выражения в скобках, отличается от 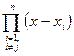 , стоящего в числителе, только наличием множителя
, стоящего в числителе, только наличием множителя 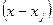 , то после сокращения дроби получим:
, то после сокращения дроби получим:
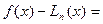
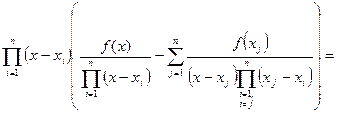
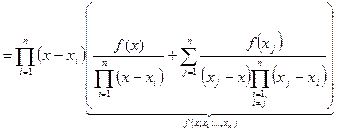 .
.
Выражение в скобках – это 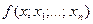 , а с учетом обозначения (185) последняя формула примет вид:
, а с учетом обозначения (185) последняя формула примет вид:
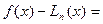
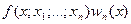 . (270)
. (270)
Пусть 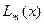 - интерполяционный многочлен Лагранжа с узлами интерполяции
- интерполяционный многочлен Лагранжа с узлами интерполяции 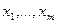 . Интерполяционный многочлен Лагранжа
. Интерполяционный многочлен Лагранжа 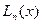 можно представить в виде:
можно представить в виде:
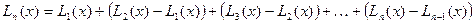 . (280)
. (280)
Поскольку 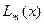 для любого
для любого 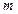 - это многочлен степени
- это многочлен степени 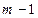 , то разность
, то разность 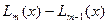 для любого
для любого 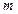 - это также многочлен степени
- это также многочлен степени 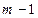 , причем его корнями являются узлы
, причем его корнями являются узлы 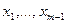 . Действительно:
. Действительно:
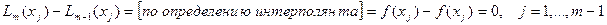 .
.
Тогда, зная все корни многочлена 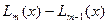 , его можно представить в виде:
, его можно представить в виде:
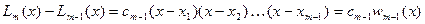 , (290)
, (290)
где 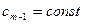 .
.
Пусть 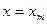 , тогда из (290) получается:
, тогда из (290) получается:
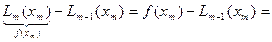
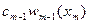 . (300)
. (300)
При 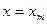 и
и 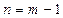 из (270):
из (270):
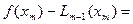
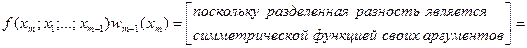
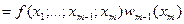 (310)
(310)
Из равенства левых частей формул (300) и (310) получаем равенство правых частей:
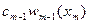
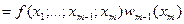 ,
,
Откуда 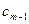
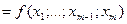 .
.
Тогда формула (290) приобретает вид:
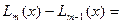
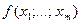
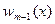 . (320)
. (320)
Подставим (320) в (280):
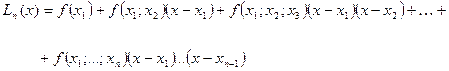 (330)
(330)
Интерполяционный многочлен, представленный в виде (330), называется интерполяционным многочленом Ньютона с разделенными разностями.
Задача. Даны значения некоторой функции 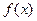 в узлах
в узлах 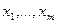 . Требуется для
. Требуется для 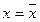 вычислить значение
вычислить значение 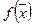 с заданной точностью
с заданной точностью 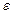 или с наилучшей возможной точностью при имеющейся информации.
или с наилучшей возможной точностью при имеющейся информации.
Предлагаемый ниже алгоритм решения задачи является довольно типичным для ситуации, возникающей в реальной практике. Невозможно предложить обоснованный алгоритм решения поставленной задачи для всех функций, поскольку про функцию ничего не известно, кроме ее значений в заданных точках. Однако, предполагая функцию гладкой, мы выводим практический критерий оценки погрешности и, основываясь на нем, строим алгоритм решения задачи.
Пусть 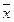 фиксировано. Предположим, что узлы интерполяции перенумерованы в порядке возрастания
фиксировано. Предположим, что узлы интерполяции перенумерованы в порядке возрастания 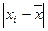 (это всегда можно сделать). Выше было получено представление погрешности интерполирования в виде (270):
(это всегда можно сделать). Выше было получено представление погрешности интерполирования в виде (270):
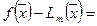
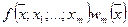 , (340)
, (340)
кроме того, из (320):
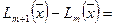
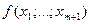
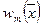 . (350)
. (350)
Сравнивая (210) и (270), из равенства левых частей этих формул получаем равенство правых частей:
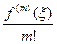
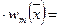
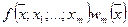 ,
,
откуда 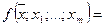
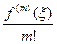 , (360)
, (360)
где 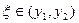 ,
, 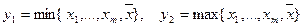 . При малых
. При малых 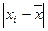 из (360) получаем:
из (360) получаем:
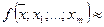
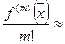
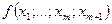 . (370)
. (370)
Тогда из (340) и (350) с учетом (370) получаем:
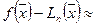
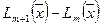 .
.
Величину 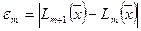 можно рассматривать как приближенную оценку погрешности интерполяционной формулы
можно рассматривать как приближенную оценку погрешности интерполяционной формулы 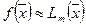 . Таким образом, для решения поставленной задачи последовательно вычисляются значения
. Таким образом, для решения поставленной задачи последовательно вычисляются значения 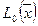 ,
, 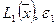 ,
, 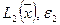 , ...; если при некотором
, ...; если при некотором 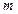 будет выполняться
будет выполняться
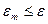 , (380)
, (380)
то вычисления прекращаются и полагают
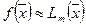 .
.
Если (380) не выполняется ни для какого 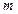 (а
(а 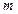 уже достигло достаточно большого значения), то находят
уже достигло достаточно большого значения), то находят
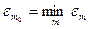
и полагают
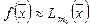 .
.
Если этот минимум достигается при нескольких 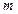 , то среди них выбирают наименьшее. Если величины
, то среди них выбирают наименьшее. Если величины 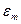 , начиная с некоторого
, начиная с некоторого 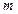 , имеют устойчивую тенденцию к увеличению, то с этого момента вычисление значений
, имеют устойчивую тенденцию к увеличению, то с этого момента вычисление значений 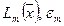 прекращают.
прекращают.
Замечание. Пусть даны значения некоторой функции 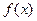 в узлах
в узлах 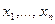 . Требуется построить интерполяционный многочлен степени
. Требуется построить интерполяционный многочлен степени 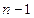 . Независимо от выбранного способа построения (при помощи решения соответствующей системы линейных уравнений, многочлен Лагранжа, Ньютона и т.д.) по имеющимся данным многочлен определяется однозначно. Лишь соображения, связанные с памятью и временем реализации могут повлиять на выбор метода построения интерполяционного многочлена.
. Независимо от выбранного способа построения (при помощи решения соответствующей системы линейных уравнений, многочлен Лагранжа, Ньютона и т.д.) по имеющимся данным многочлен определяется однозначно. Лишь соображения, связанные с памятью и временем реализации могут повлиять на выбор метода построения интерполяционного многочлена.
Дата добавления: 2015-03-20; просмотров: 1096;
