Разделенные разности и их свойства

1. Какие задачи приводят к необходимости приближения функции? Можно ли в принципе обойтись без приближения функций? Почему?

2. Что такое интерполирование? Чем оно отличается от других способов приближения функции?

3. Что такое узлы интерполяции? Сколько их должно быть? Каким правилам подчиняется выбор узлов интерполяции?

4. Каким образом выбираются базисные функции для интерполирования?

5. Каким образом нахождение интерполянта сводится к решению системы линейных уравнений? Какова вычислительная сложность такого способа построения интерполяционного многочлена по 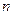узлам?

6. Какие базисные функции используются при построении интерполяционного многочлена Лагранжа?

7. Вывод формулы интерполяционного многочлена Лагранжа.

8. Оценка погрешности интерполяционного многочлена Лагранжа в произвольной точке.

9. Пусть значения функции 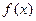заданы в узлах 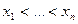. По имеющимся данным построен интерполяционный многочлен степени 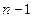с использованием формулы Лагранжа, а также интерполяционный многочлен степени 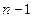при помощи решения системы линейных уравнений (130) для определения коэффициентов интерполяционного многочлена. Как связаны между собой полученные интерполяционные многочлены? Ответ пояснить.

10. Что происходит с «качеством» интерполяции при росте степени интерполяционного многочлена? Ответ пояснить.

11. Вывести формулу числа арифметических операций для построения интерполяционного многочлена Лагранжа по 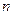узлам интерполяции.

12. Построить интерполяционный многочлен второй степени для функции 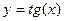на сегменте 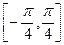двумя способами. Сравнить полученные интерполянты. Результат пояснить.

Литература.

1.Нэш

2.Бахвалов новый

Разделенные разности и их свойства

Обобщением понятия производной является понятие разделенной разности. Разделенные разности нулевого порядка просто совпадают со значениями функции ; разности первого порядка определяются равенством:

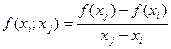. (230)

Если вспомнить определение производной функции в точке :

,

и сравнить с (230), то становится очевидной аналогия разделенной разности с производной.

Разделенные разности второго порядка определяются равенством:

,

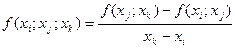и вообще, разности 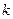-го порядка определяются через разности 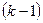-го порядка в соответствии с формулой:

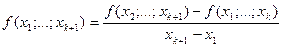. (240)

Лемма. Справедливо равенство:

. (250)

Доказательство. Для доказательства воспользуемся методом математической индукции. Проверим выполнение (250) для :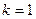

;

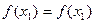для :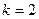

,

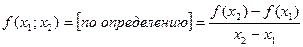а ,

что говорит о выполнении (250) для .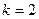

Предположим, что для для 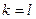формула (250) доказана. Покажем, что тогда она верна и для , т.е. 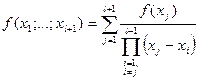, а коэффициент при 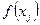действительно равен

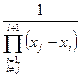. (255)

Для этого преобразуем выражение для 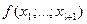, которое получается по определению разделенной разности 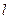-го порядка:

(260)

Если 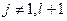, то 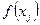присутствует в обеих суммах, стоящих в скобках в правой части формулы (260). Коэффициенты при 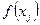в первой и второй суммах соответственно равны:

, .

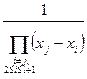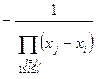Тогда полный коэффициент при 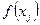в правой части формулы (260) равен:

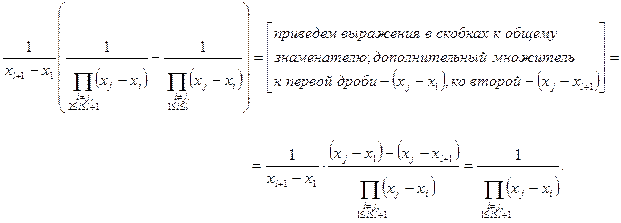
что в точности отвечает (255).

Для 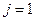или значение 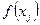входит только в одну сумму в скобках в правой части формулы (260) и коэффициент при нем, как легко убедиться, также имеет требуемый вид (255).

Из предыдущей леммы вытекает, что разделенная разность 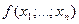является симметрической функцией своих аргументов 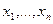, т.е. не меняется при любой их перестановке.

Если функция 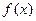задана в точках 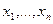, то таблицу

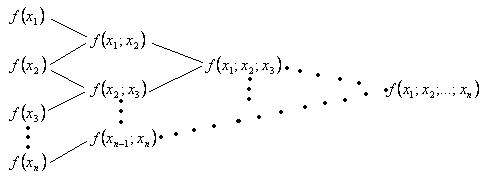
называют таблицей разделенных разностей. Таблица разделенных разностей часто используется для удобства при вычислении значения 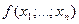, а также всех разделенных разностей меньшего порядка.