Интерполяционные сплайны

Непрерывная функция не всегда может быть хорошо приближена интерполяционным многочленом Лагранжа, Ньютона и т.д., основанным на глобальной интерполяции.

С середины 60-х годов популярность приобрел альтернативный подход: использование для приближения кусочно-полиномиальных функций, или сплайнов.

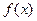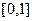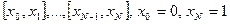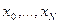Для определенности будем говорить о приближении функции на отрезке . Разобьем его на части , где - узлы интерполирования, и обозначим это разбиение через 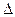. Назовем сплайном 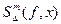порядка 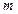функцию, являющуюся многочленом степени 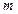на каждом из отрезков 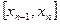, причем на каждом отрезке 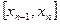свой многочлен 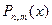(в обозначении 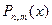первый индекс 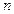указывает на частичный отрезок, для которого построен многочлен, а второй индекс 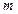- на степень многочлена),т.е.

при : =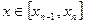

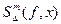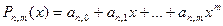
и удовлетворяющую условиям непрерывности производных до порядка 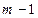в точках :

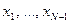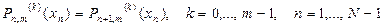. (390)

Всего имеется 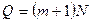неизвестных коэффициентов многочленов 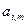: количество частичных сегментов - 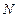, на каждом частичном сегменте свой многочлен степени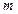 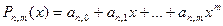, который определяется своими 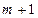коэффициентами. Соотношение (390) – это система 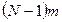линейных алгебраических уравнений. Понятно, что пока количество уравнений в общем случае меньше количества неизвестных. Другие уравнения для для искомых коэффициентов многочленов получаются из условия близости сплайна к приближаемой функции и из некоторых дополнительных условий.

Рассмотрим задачу приближения функции 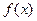линейным сплайном ( 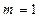), тогда общее число неизвестных 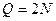. Поскольку искомый сплайн 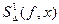совпадает со значением 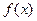в узлах 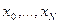, то получаем систему уравнений:

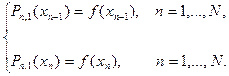
Эта система распадается на системы уравнений относительно коэффициентов отдельных многочленов:

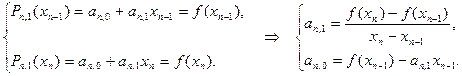
Многочлен 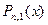является интерполяционным многочленом первой степени с узлами интерполяции .

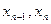Интерполяционный сплайн первой степени представлен на рис.1.

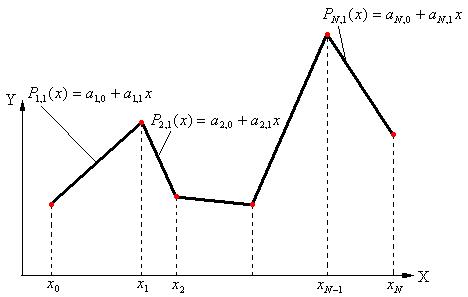
Рис.1.

Интерполяционный сплайн первой степени обладает следующим очень важным свойством: если между узлами 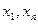появляются дополнительные точки-узлы, в которых известны значения приближаемой функции 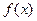, то интерполянт улучшается, т.е. приближается к исходной функции. Более того, если 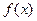имеет непрерывную вторую производную, то можно доказать, что

,

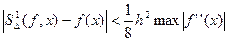где 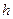- наибольшая из длин частичных сегментов. Важность этого результата состоит в том, что выражение для оценки погрешности содержит лишь вторую производную и не зависит от числа узлов. Если удвоить число равномерно расположенных узлов, уменьшив тем самым 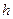в два раза, то погрешность для нового интерполянта составит около ¼ погрешности старого. Таким образом, выбрав достаточно много узлов, ошибку интерполяции можно сделать сколь угодно малой. Конечно, на практике интерполируемая функция редко бывает известна, а добавление дополнительных точек является роскошью. Однако подобные утверждения о сходимости дают нам уверенность в этом методе, особенно с негарантированно сходящейся глобальной полиномиальной интерполяцией.

Хотя интерполяционный сплайн первой степени решает проблему, возникающую при глобальной полиномиальной интерполяции – обладает сходимостью при увеличении количества узлов, но порождает при этом другую проблему – недостаток гладкости: график 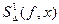имеет изломы. Поэтому на практике, как правило, используют интерполяционные сплайны более высоких степеней – чаще всего третьей степени 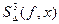. Они обеспечивают высокую точность приближения, имеют простую численную реализацию и достаточную гладкость.

Вопросы