Полиномиальная интерполяция

В силу исторических и практических причин наиболее важным для интерполяции классом базисных функций является множество многочленов. У многочленов есть очевидные преимущества перед другими функциями: их легко вычислять, их легко складывать, умножать, интегрировать и дифференцировать.

Любую непрерывную функцию 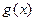можно приблизить на отрезке некоторым многочленом 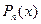. Это следует из аппроксимационной теоремы Вейерштрасса: если 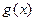произвольная непрерывная на сегменте 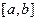функция, то для любого 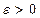найдется такой многочлен 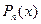степени 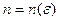, что

.

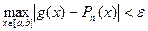Хотя некоторые доказательства теоремы Вейерштрасса являются конструктивными (в процессе доказательства строится нужный многочлен), обычно в результате получается многочлен такой высокой степени, что использовать его на практике невозможно. Более того, теорема Вейерштрасса ничего не говорит о существовании удовлетворительного интерполирующего многочлена для заданного набора данных. И хотя важно знать, что некоторый полином приближает 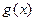с предписанной точностью на всем отрезке 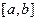, нет никакой гарантии, что этот многочлен удастся найти с помощью практического алгоритма.

Выберем в качестве базисных функций неотрицательные целые степени переменной :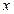

.

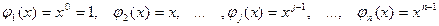Система (110) будет иметь вид:

,

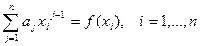где

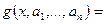
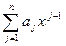(125)

- интерполяционный многочлен степени ,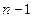

или

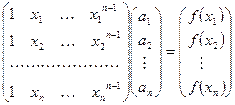. (130)

Все 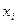различны, решение системы (130) существует и единственно, следовательно существует единственный интерполяционный многочлен вида (125).

Поскольку все множество данных: набор узлов интерполяции 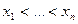и значений функции 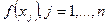, в этих узлах, включается в одну полиномиальную интерполирующую функцию 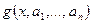, то 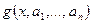называется глобальным интерполянтом этих данных.