Постановка задачи приближения функций

Сохраним уравнение

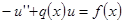, но вместо условий Дирихле возьмем условия Неймана: . Задача

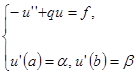
называется задачей Неймана для уравнения Гельмгольца.

Дискретизации здесь требует не только уравнение, но и граничные условия, для которых выберем простейший способ аппроксимации:

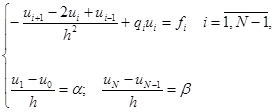
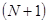уравнений и 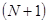неизвестных.

Матрица СЛАУ и вектор правой части соответственно имеют вид:

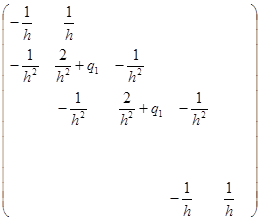
Матрица сохраняет трёхдиагональную структуру.

Рассмотрим подробнее уравнение СЛАУ:

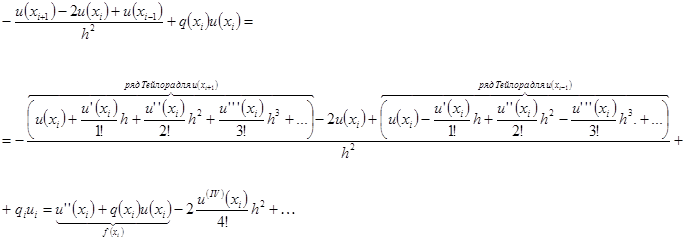
Тут 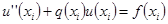и 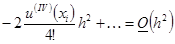, т.е. уравнение имеет порядок аппроксимации .

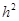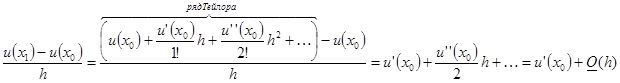
- граничные условия имеют порядок аппроксимации .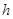

Постановка задачи приближения функций

1. Простейшая задача, приводящая к приближению функции, заключается в следующем. В дискретные моменты времени 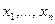наблюдаются значения функции 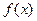; требуется восстановить ее значения при других 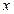. Подобная задача может возникнуть при разных обстоятельствах. Например, если 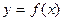алгебраическое выражение, содержащее только арифметические операции, то выполняя эти операции мы можем точно найти значение 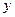, которое соответствует любому значению 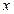. Но если, например, 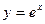, то невозможно вычислить 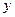, выполняя простые арифметические операции над 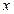(во всяком случае, невозможно точно вычислить 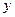, выполняя конечное число таких операций). В этом случае приходится прибегать к таблице, которая дает значения 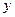, отвечающие нескольким выбранным значениям 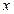, например, как табл.1.

Таблица1 –

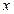
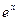
-1 -10 -20	2.718282 22026.46 4.8516520*108 0.3678795 4.5399930*10-5 2.0611537*10-9

Возникает вопрос, как можно найти значения функции 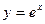для аргументов 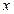, лежащих в промежутках между табулированными значениями. Ответ на этот вопрос дается теорией интерполяции, которую в ее наиболее элементарном аспекте можно назвать «наукой чтения между строк математической таблицы».

Подобная задача возникает также в следующем случае. По ходу вычислений на ЭВМ приходится многократно вычислять одну и ту же сложную функцию в различных точках. Вместо ее непосредственного вычисления иногда целесообразно вычислить ее значения в отдельных выбираемых нами по своему усмотрению точках, а в других точках вычислять по каким-то простым формулам, используя информацию об этих известных значениях.

Интерполяция – это часто встречающаяся операция как при работе на компьютерах, так и в повседневной жизни. Например, у нас есть данные, полученные с большими затратами всего в нескольких точках, нам необходимо определить величины между этими точками: данные переписи населения, которая проводится раз в 10 лет.

Мы часто проводим интерполяцию, не отдавая себе в этом отчета, например, при построении графика функции, получая на координатной плоскости несколько точек, принадлежащих графику, соединяем их некоторой кривой – интерполируем.

Формально понятие интерполяции вводится следующим образом. Пусть из каких-то дополнительных соображений известно, что приближающую для 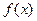функцию нужно искать в виде:

.

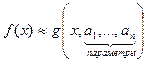Если параметры 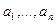определяются из условия совпадения 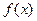и приближающей функции 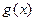в точках 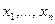, которые называются узлами интерполяции, т.е.

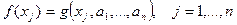, (100)

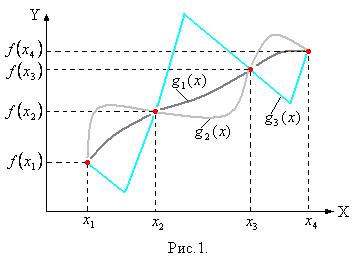то такой способ приближения функции называется интерполированием или интерполяцией, а 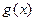- интерполирующей функцией или интерполянтом (рис.1). Из рис.1 видно, что узлы интерполирования сами по себе не могут определить интерполянт. Для фиксированного набора данных существует бесконечно много интерполянтов (на рис.1 приведены 3 возможных интерполянта).

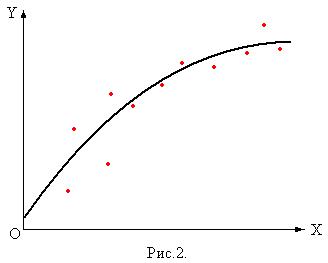
Необходимо отметить, что интерполяция может быть полезной только в том случае, когда исходные данные 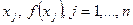, не содержат ошибок. Экспериментальные данные, содержащие ошибки часто аппроксимируют (приближают) иначе. На рис.2 показаны экспериментальные данные и функция, которая описывает эти данные лучше, чем любой интерполянт.

Далее будем заниматься интерполяцией функций, зависящих только от одной переменной.

Пусть задан набор узлов интерполяции 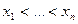и значений функции 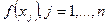, в этих узлах. Необходимо построить интерполянт для функции 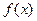, который дает приемлемые значения при 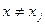. Это нельзя сделать абсолютно строго, поскольку все зависит от процесса, порождающего данные, нашего представления о приемлемости таких значений и т.д. При стандартном подходе к процессу интерполирования, в первую очередь, задают набор базисных функций 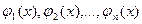. Они могут быть выбраны из соображений опыта, по рекомендации или на основе математической или физической интуиции; в любом случае предполагается, что они известны. Интерполирующая функция ищется в виде:

,

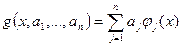где параметры – числа - пока неизвестны. Эти параметры определяются из условия интерполяции (100):

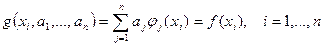. (110)

По сути своей (110) – это система 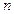линейных уравнений с 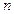неизвестными :

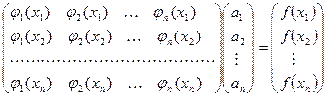. (120)

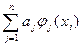Нахождение интерполянта свелось к решению системы линейных уравнений: найдя , и подставив их в из (110), получим искомую интерполирующую функцию.