Рег. волны помехи при сейсморазведке МОВ 5 страница
Они обладают опорными свойствами, т.е. следятся практически по всему региону, однако динамическая выразительность отдельных волн резко меняется по латерали, что связано с литологическими особенностями осадков в этой части разреза.
ОГ Г- наиболее устойчивый из верхнемеловых ОГ. На его формирование оказывает влияние кровля сеноманского яруса (подошва глин кузнецовской свиты). Горизонт Г прослеживается обычно на несколько десятков метров выше или ниже этой геологической границы.
Горизонт С-сеноманские глинисто-кремнистые образования.
Горизонт Э-отложения эоцена
Менее амплитудные и протяженные ОГ, получили название дополнительных. Еще на первых этапах геофизического изучения ЗС были прослежены такие горизонты в нижней-средней юре и неокоме. Первые получили индекс Т, (Т1,Т2, Т3,Т4) от названия “тюменская свита”, к которой они были приурочены. Неокомские ОГ индексировались по-разному – В (по последовательности, снизу вверх: А – подошва юры, Б –верхняя юра, В – неоком, Г – турон) или ‘d” (дополнительные).

Вертикальная и латеральная разрешающая способность сейсморазведки
Под разрешающей способностью понимают такое минимальное расстояние между двумя различными объектами, на котором они еще различаются как два отдельных объекта. Различают два направления:
-разрешающая способность по вертикали (по времени, по глубине);
-разрешающая способность по горизонтали (от трассы к трассе вдоль профиля, или по площади).
Под разрешающей способностью по вертикали понимают способность выделения отдельных пропластков в многослойной среде, она зависит от уровня помех, литологического состава пород, подстилающих и перекрывающих геологический объект, частотного спектра сейсмических волн, мощности геологических тел, способности интерпретатора улавливать незначительные изменения формы сигнала и т.д.
Единственной управляемой величиной, влияющей на длину волны, следовательно, и на разрешающую способность по вертикали, является частота, т.е. разрешающую способность можно увеличить, записывая более высокие частоты. Достигнуть этого можно, если использовать высокочастотные источники и сохранять высокие частоты при записи и обработке.
При правильной обработке разрешенность по вертикали может составлять величину от 1/8 до 1/4 длин волн, а при отсутствии шумов и при относительно простом геологическом строении можно выделять и более близко расположенные объекты. Отдельные отражения от кровли и подошвы пласта можно различить, пока его мощность не станет меньше 1/8 длины волны главной гармоники частотного спектра импульса. Эта величина называется критической разрешающей мощностью. Если мощность пласта меньше этой критической величины, длина полупериода отраженного сигнала (расстояние между экстремумами, соответствующими его кровле и подошве) перестает зависеть от мощности пласта. В Западной Сибири в интервалах глубин до 2-3 км, при стандартной методике сейсморазведки МОВ, возможно раздельное прослеживание пластов мощностью не менее 15-20 м.
Под разрешающей способностью по горизонтали (латерали) понимают способность выявления латеральных изменений в пропластках в многослойной среде.
При распространении сейсмической волны от точечного источника в среде образуется область возмущения, ограниченная передним и задним фронтами волн, которые являются сферическими поверхностями. Оба фронта распространяются в среде с одинаковой скоростью. Область возмущения во времени соответствует длительности исходного импульса (1,5 периода волны) и находится за волновым фронтом. При падении фронта волны на отражающую поверхность происходит отражение некоторой его части, расположенной между точками пересечения отражающей поверхности со сферической поверхностью, отображающей границу области возмущения. На рис показана область возмущения глубиной в 1/4 длины волны. Часть отражающей поверхности, ограниченная линией пересечения с фронтом волны, представляет собой площадку, участвующую в образовании отражения. Эта площадка называется первой зоной Френеля. Сигнал, отражённый от этой площадки, прибудет к сейсмоприёмнику, расположенному на дневной поверхности в точке взрыва (источника), в течение одного полупериода и будет интерферировать без ослабления. Сигнал, отражённый от поверхности за пределами первой зоны Френеля, прибудет к сейсмоприёмнику с опозданием на 1/2 длины волны относительно первого вступления отражения и будет ослаблен. Радиус первой зоны Френеля можно рассчитать по формуле
Rф » 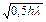 ,
,
где h – глубина до исследуемой границы, l - длина волны, Rф – первая зона Френеля
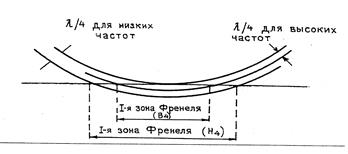
Рис. Отражение сферической волны от плоской границы раздела
Радиус зоны Френеля увеличивается с глубиной и с уменьшением частоты.
Суммарный интерференционный отражённый импульс формируется не плоскостью отражающей поверхности, а некоторым трёхмерным объёмом, называемым диском Френеля. Диаметр этого диска равен эффективной ширине первой зоны Френеля, а высота – половине эффективной длительности падающего импульса. Ещё одним способом анализа разрешающей способности по латерали является анализ дифракции волн. При приближении размеров объекта к диаметру первой зоны Френеля и последующем его уменьшении проявление объекта видоизменяется и приобретает характер дифрагированного сигнала от точки. Если две точки удалены друг от друга на расстояние равное диаметру первой зоны Френеля, эти точки будут «видны» на сейсмограммах не как одна, а как две разные точки
Сокращение радиуса зоны френеля непосредственно связано с повышением разрешенности. Размер зоны Френеля зависит от частоты сейсмических колебаний, от расстояния до источника и от кривизны фронта волны
2. Метод полумаксимума, как экспресс-метод количественной интерпретации магнитных аномалий.
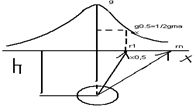 ∆gш=fMh/r3
∆gш=fMh/r3
gmax=fM/h2 r0,5=√x0,52+h2 fMh/(x0,52+h2)=fM/2h2 2h3=( x0,52+h2)3/2 21/3h=( x0,52+h2)1/2 h=1/21/3√ x0,52+h2
h2= (x0,52+h2)/22/3 22/3h2=(x0,52+h2) 22/3h2 -h2= x0,52 h2(22/3-1)=x0,52 h=x0,5/√22/3-1=1,47x0,5
метод используется для экспресс-оценки глубины залегания аномалиеобразующего объекта.
| объект | h/x1/2 |
| Вертикальный пласт | 0.58 |
| Горизонтальный круговой цилиндр | |
| Вертикальный цилиндр | |
| шар | 1.47 |
Глубина определяется до особой точки объекта – для шара и горизонтального цилиндра это центр, для вертикального пласта и стержня – верхняя кромка.
3. Основные уравнения Максвелла для постоянного тока, их характеристика.
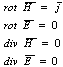
Первое уравнение показывает зависимость вихревого магнитного поля Н от плотности тока проводимости j, второе постулирует факт, что в стационарном поле нет вихревых индукционных токов, третье и четвёртое - уравнения непрерывности магнитных и электрических силовых линий в отсутствие объёмно распределенных и сторонних зарядов. Закон Ома в дифференциальной форме 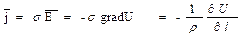 .
.
Уравнение годографа МОВ и МОВ ОГТ однократных волн.
Принципиальную сущность МОГТ составляет идея многократного прослеживания одних и тех же отраженных волн при различном взаимном положении источников и приемников упругих колебаний. Широкое применение систем многократных перекрытий в практике сейсморазведочных работ обусловлено возможностью реализации в процессе обработки алгоритмов, обеспечивающих существенное повышение сигнал/помеха за счет ослабления как нерегулярных колебаний, так и регулярных волн-помех типа кратных, обменных и др.
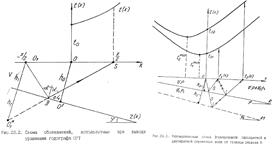
В основу большинства таких алгоритмов заложены кинематические особенности отраженных (однократных и многократных) и дифрагированных волн. Кроме того, кинематические характеристики сейсмических волн, регистрирующихся на сейсмограмме ОГТ, играют важную роль при расчетах и выборе параметров систем наблюдений. Сейсмограммы (с/г), обрабатываемые по методике ОГТ, представляют собой выборку каналов (трасс) из сейсмограммы общей точки возбуждения (ОТВ), полученных в процессе многократного профилирования. Годографы сейсмических волн, прокоррелированные (выделенные) на сейсмограмме ОГТ в соответствии с принципами симметрии относительно центра расстановки – общей средней точки (ОСТ) называют годографами ОГТ. График, выражающий зависимость времени t прихода волны от координат x и y точек наблюдения называют годографом. Пусть плоская отражающая граница залегает под углом φ к горизонту. Покрывающая ее толща однородна и характеризуется всюду одинаковой скоростью V. Начало координат разместим в точке О, которую будем называть общей средней точкой (ОСТ). Глубину по нормали от центра системы наблюдений до границы раздела примем равной h0. В точке на профиле наблюдений, имеющей координату минус х/2, поместим источник колебаний. В точке профиля х/2 (расположенной симметрично относительно ОСТ) поместим приемник колебаний. Требуется определить время пробега отраженной волны от источника до приемника. Эту зависимость, полученную в виде формулы, будем называть уравнением годографа ОГТ. При выводе искомой формулы будем использовать уже известное нам уравнение годографа отраженной волны для общей точки взрыва ОТВ. Для этого временно совместим начало новой системы координат с пунктом взрыва О1. Глубина по нормали до отр.границы в этой точке профиля равна
h1=h0-x/2sin φ. (1)
Как известно, уравнение годографа ОТВ, определяющее время пробега волны по траектории О1DS, в этой системе координат и обозначений будет иметь вид:
t(x)=1/V*√x2+4h1x sin φ +4h12 (2).- МОВ
Подставив в ур-е (2) глубину h1 из (1), будем иметь:
t(x)=1/V*√x2+4x (h0-x/2 sin φ) sin φ+4(h0-x/2 sin φ)2 = 1/V*√x2 - х2sin2 φ+4h02 =1/V*√4 h02 + х2cos2 φ (3).
После внесения под знак радикала и с учетом нижеследующих общепринятых обозначений: t0=2h0 / V; Vогт= V/cosφ (4) будем иметь следующее окончательное выражение для уравнения годографа ОГТ
t(x)= √ t02 + x2/Vогт2 -МОВ ОГТ
Следует всегда помнить, что х – расстояние от ПВ до ПП. Из анализа уравнения годографа ОГТ следуют такие важные выводы: годограф ОГТ однократно отраженной волны для однородной покрывающей среды представляет собой гиперболу с мин. в точке симметрии – точке ОСТ; - С увеличением угла наклона отражающей границы крутизна годографа уменьшается; - форма годографа не зависит от знака угла наклона отражающей границы; - для фиксированного t0 годограф ОГТ является функцией только одного параметра – параметра Vогт, который принято называть скоростью ОГТ, фиктивной скоростью и т. п.
Волны Р и S распространяющиеся от источника вниз и отразившиеся от границы, наз-т однократно-отраженными (отраженными). Нижние точки отражения могут соответствовать одной и той же границе – полнократная волна.
2. Намагниченность: ее природа и носители. Виды намагниченности.
Источник намагниченности – магнитные свойства горных пород, которые основаны на спиновых и орбитальных моментах электронов.
При наведении поля электроны упорядочиваются:
Намагниченность определяется как отношение суммы магнитных моментов к сумме элементарных объемов вещества.
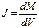 ,
,
Где М – магнитный момент, V – объем. [J]=A/м (СИ), в (Сгс) размерности не имеет. JСИ=103JСГС
Если направление модуль-вектора J постоянно, то намагниченность однородная.
Виды намагниченности:
1. Индуктивная или наведенная намагниченность (вызвана внешним полем и исчезает при его снятии). Обозначается Ji
2. Остаточная намагниченность (характерна для ферромагнетиков, т.е. остается при снятии поля). Обозначается Jn
Характеристика магнитных свойств вещества:
Q=Jn/Ji – коэффициент Кёнигсбергера (им характеризуется естественная остаточная намагниченность)
3. Основные уравнения Максвелла для переменного тока, их характеристика.
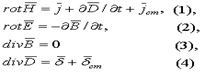
Первое уравнение – дифференциальное выражение закона полного тока, указывает на связь вихревого магнитного поля с токами проводимости и смещения. Второе уравнение – дифференциальное выражение закона электромагнитной индукции – всякое изменение магнитной индукции В возбуждает в проводящей среде вихревое электрическое поле Е. Направление вихря Е таково, что возникший индукционный ток и связанное с ним вторичное магнитное поле противодействуют изменению магнитной индукции, на что указывает знак минус. Третье и четвёртое уравнения выражают непрерывность (замкнутость) магнитных и электрических силовых линий в отсутствие сторонних зарядов.
Цифровое кодирование сейсмической записи, выбор частоты кодирования (теорема Котельникова), частота Найквиста, появление « зеркальных» частот, способ подавления « зеркальных» частот.
Цифровое кодирование сейсмической записи- выбор частоты кодирования (теорема Котельникова) – если спектр X(ω) некоторая функция X(t) задан в ограниченной полосе частот - 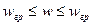 то функция X(t) можно полностью восстановить по ее отсчетам заданным через интервал
то функция X(t) можно полностью восстановить по ее отсчетам заданным через интервал 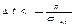 эта теорема лежит в основе выбора шага дискретизации
эта теорема лежит в основе выбора шага дискретизации 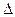 t. Из теоремы вытекает , что если самая высокая частота спектра X(w) функции X(t) равна ωгр, , то максимальная частота шагом дискретизации
t. Из теоремы вытекает , что если самая высокая частота спектра X(w) функции X(t) равна ωгр, , то максимальная частота шагом дискретизации 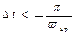 . При котором у спектральной компоненты К ωгр на частоте ωгр получим 2 отсчета на период. Зависимость от фазового сдвига рассматриваемой компоненты эти 2 отсчета попадают либо на экстремум либо на промежуточные синусоиды соответствует компоненте X(ωгр) спектра. Таким образом для абсолютно точного соблюдения теоремы Котельникова необходимо , чтобы функция X(ω) была бесконечно протяженной, а условия X(ω)=0, при ω<-ωгр ω>ωгр соблюдались строго. При этих условиях выбирается шаг дискретизации гр
. При котором у спектральной компоненты К ωгр на частоте ωгр получим 2 отсчета на период. Зависимость от фазового сдвига рассматриваемой компоненты эти 2 отсчета попадают либо на экстремум либо на промежуточные синусоиды соответствует компоненте X(ωгр) спектра. Таким образом для абсолютно точного соблюдения теоремы Котельникова необходимо , чтобы функция X(ω) была бесконечно протяженной, а условия X(ω)=0, при ω<-ωгр ω>ωгр соблюдались строго. При этих условиях выбирается шаг дискретизации гр 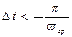 (1)между тем сейсмические трассы являются ограниченными во времени функциями , а еще в большей степени относятся к отдельным сейсмическим сигналам, также функции не могут иметь ограничение спектра, лишь стой или иной степени приближенности можно говорить о том, что спектр задан в конечном интервале от ω до ωгр. Поэтому и теорема Котельникова к сейсмосигналам лишь в той или иной степени. Установлено что во времени сейсмозаписи требуется выбирать меньше шаг дискретизации, что принесет в теорему Котельникова бесконечно длинную фазу. В частности по теореме Котельникова шаг дискретизации =2мс, можно у бесконечно протяженной кривой восстановить все частоты в пределах ± 250 Гц, а
(1)между тем сейсмические трассы являются ограниченными во времени функциями , а еще в большей степени относятся к отдельным сейсмическим сигналам, также функции не могут иметь ограничение спектра, лишь стой или иной степени приближенности можно говорить о том, что спектр задан в конечном интервале от ω до ωгр. Поэтому и теорема Котельникова к сейсмосигналам лишь в той или иной степени. Установлено что во времени сейсмозаписи требуется выбирать меньше шаг дискретизации, что принесет в теорему Котельникова бесконечно длинную фазу. В частности по теореме Котельникова шаг дискретизации =2мс, можно у бесконечно протяженной кривой восстановить все частоты в пределах ± 250 Гц, а 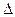 t =4±125 Гц, тогда как у ограниченной по времени сейсмозаписи для воспроизведения тех же частот следует выбирать
t =4±125 Гц, тогда как у ограниченной по времени сейсмозаписи для воспроизведения тех же частот следует выбирать 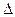 t =1-2 мс( 250-500Гц)
t =1-2 мс( 250-500Гц)
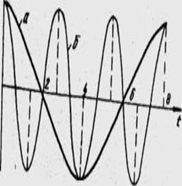
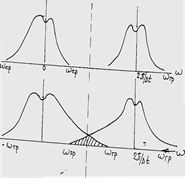
рис 2 рис1
из рисунка 1 видно что ωгр<π/ Δ t, то на главный период побочные периоды не накладываются. Участки побочных периодов накладываются на главный период на частоте ω<π/ Δ t и носят название зеркальных частот. Явление наложения зеркальных частот можно пояснить на следующем рисунке.
Пусть некоторая компонента X(ω1) имеет функцию ω<π/ Δ t из рисунка видно , что дискретность этой компоненты приводит к появлению фиктивной синусоиды частот , ω2 меньше чем π/ t которая будет суммироваться с тем или иным фазовым сдвигом по частоте ω1 = ω2 1- отрезок временной кривой полученный с реальной спектральной компонентой больше, чем π/ t ;2- отрезок временной фиктивной кривой зеркальной компоненты. 3,4,5,- точки дискретного отсчета с частотой ω1 . если наложение зеркальных частот не происходит , то выбирая тот или иной интервал по оси частот -π/ t до π/ t можно выделить участок спектра X(ω1 равный ( с точностью до постоянного множителя) спектру непрерывной функции X(ω). Это дает возможность пользуясь обратным преобразованием Фурье 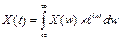
В интервале частот , где ω2< π/ Δ t < π/ Δ t восстановить исходную функцию X(ω).. если же wгр > π/ Δ t и произошло наложение зеркальных частот, то ни никаком участке оси часто мы не найдем такого периодического спектра X(ω)= X(ω). Это в свою очередь лишает возможности восстановить непрерывную функцию X(t) точно, таким образом частота 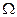 =± π/ Δ t представляет собой важную границу , если не нулевые ординаты главный период спектра X(ω) не выходит за пределы этой границы, то возможно точное восстановление этой функции, если выходят , то точное восстановление не возможно, такую частоту называют – частота Найквиста.
=± π/ Δ t представляет собой важную границу , если не нулевые ординаты главный период спектра X(ω) не выходит за пределы этой границы, то возможно точное восстановление этой функции, если выходят , то точное восстановление не возможно, такую частоту называют – частота Найквиста.
частота Найквиста- граничную частоту ωN принято называть частотой Найквиста в честь американского физика, частота Найквиста равна половине частоты квантования 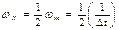 Поскольку строгое определение максимальной частоты спектра сейсмического сигнала затруднено и не всегда возможно , принимают другое условие – погрешность кусочно- линейной аппроксимации квазигармонических сигналов . Можно показать , что максимальная погрешность кусочно- линейной аппроксимации синусоидальных сигналов с частотой ω определяется формулой:
Поскольку строгое определение максимальной частоты спектра сейсмического сигнала затруднено и не всегда возможно , принимают другое условие – погрешность кусочно- линейной аппроксимации квазигармонических сигналов . Можно показать , что максимальная погрешность кусочно- линейной аппроксимации синусоидальных сигналов с частотой ω определяется формулой: 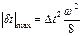 . Если принять , что искажения, вызываемые квантованием по времени, не должны превышать 3 дБ, то следует
. Если принять , что искажения, вызываемые квантованием по времени, не должны превышать 3 дБ, то следует 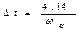 . Поскольку это условие более жесткое, то на практике принимают, что частота квантования всегда должна превосходить максимальную частоту спектра регистрируемых колебаний в четыре раза. При восстановлении аналоговых, квантованных по времени сигналов возникают искажения, связанные с появлением ложных помех. В области спектров сигналов, ограниченной частотой Найквиста ωN, будут формироваться помехи, обусловленные компонентами спектра сигнала на частотах выше ωN. Это означает , что если в спектре квантуемого сигнала имеются гармоники более высокой частоты, чем частота Найквиста, частоты ωN+Δω, то при квантовании во времени они восстанавливаются как гармоники более низкой частоты ωN-Δω. Возможность такого варианта на рис 2
. Поскольку это условие более жесткое, то на практике принимают, что частота квантования всегда должна превосходить максимальную частоту спектра регистрируемых колебаний в четыре раза. При восстановлении аналоговых, квантованных по времени сигналов возникают искажения, связанные с появлением ложных помех. В области спектров сигналов, ограниченной частотой Найквиста ωN, будут формироваться помехи, обусловленные компонентами спектра сигнала на частотах выше ωN. Это означает , что если в спектре квантуемого сигнала имеются гармоники более высокой частоты, чем частота Найквиста, частоты ωN+Δω, то при квантовании во времени они восстанавливаются как гармоники более низкой частоты ωN-Δω. Возможность такого варианта на рис 2
на рисунке 2 видно, что численные значения синусоиды частоты 125 Гц совпадают с численным значением синусоиды частоты 375 Гц . Отсюда следует, что высокочастотный сигнал 375 Гц будет восприниматься устройством также, как и сигнал частоты 125 Гц. Заметим , что частота 375 Гц является зеркальным отображением частоты 125 Гц относительно частоты Найквиста, которая в этом примере равна 250 Гц, поскольку частота квантования 500 Гц. Для устранения помех, сейсмические сигналы до квантования во времени должны быть подвергнуты низкочастотной фильтрации, антиаляйсинг- фильтр(фильтр низкой частоты) должен иметь граничную частоту, меньшую частоты квантования ωгр<ωкв и значительную крутизну среза.
Задачи и методы трансформаций гравимагнитных аномалий.
Задачи трансформаций:
1) решение или проведение качественнйо интерпретации;
2) выделение из поля аномалий, обусловленных влиянием объектов, расположенных на разной глубине.
Методы трансформации:
1) осреднение (выделяют g региональную);
2) пересчет в верхнее и нижнее полупространство (строится на основе аналитического продолжения гармонических функций);
3) вычисление высших производных (фильтры высоких частот);
4) частотное преобразование (частотная фильтрация).
3. Основные характеристики гармонически изменяющегося электромагнитного поля.
1) комплексное волновое число 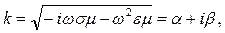
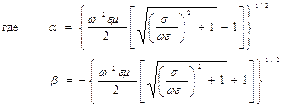
а) квазиволновое приближение (высокие частоты, плохо проводящая среда) 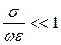
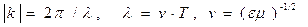
б) квазистационарное приближение (низкие частоты, проводящая среда) 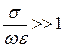
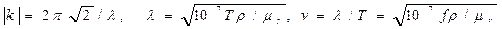
2) эффективная глубина проникновения вихревых токов зависит от λ или ω (ω=2π/Т) в реальных средах
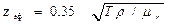
3) параметр поля p – мера удаления пункта наблюдения от источника, ею является относительное численное расстояние: 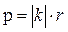 Величина, обратная квадрату параметра p, пропорциональна удельному сопротивлению среды:
Величина, обратная квадрату параметра p, пропорциональна удельному сопротивлению среды:
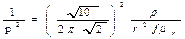
p << 1 – ближняя зона, p >> 1 – дальняя (волновая) зона
Основы динамического анализа до суммирования (AVO, AVA - анализ)
AVO-анализ (amplitude variations offset) – анализ амплитуд отражения в зависимости от угла падения (удаления).
В настоящее время динамическая интерпретация выполняется, в основном, по сумотрассам, т.е. информация об амплитудах исходных трасс теряется после суммирования. Для детального анализа амплитудных вариаций, связанных с характеристиками горных пород, необходимо использовать данные до суммирования. Основа AVO-анализа – угловой коэффициент отражения. При ненулевом угле падения акустический коэффициент отражения R( 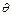 ) определяется уравнением:
) определяется уравнением:
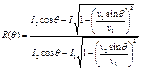
где q - угол падения, I – акустический импеданс для 1 и 2 слоя, v2, v1 – скорость в пласте и в покрывающих породах.
Изменение значений акустического коэффициента отражения от угла падения для газонасыщенного песчаного пласта, перекрытого глиной.
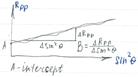
Основным условием использования AVO-анализа является то, что некоторые ловушки углеводородов (в основном газонасыщенные пески) дают в отражённых волнах увеличение амплитуды отражения с увеличением удаления ПВ-ПП, в то время как ненасыщенные участки дают несущественное увеличение или даже резкое уменьшение амплитуды с ростом удаления. Это метод анализа используется для определения AVO-аномалий на больших массивах данных и называется intercept-gradient или АВ-метод. Он основан на математическом положении, что коэффициент отражения упругой Р-волны может быть аппроксимирован как:
Rpp@A+Bsin2(q),
где А – значение амплитуды при нормальном падении (нулевое удаление), В – градиент.
Чтобы использовать эту связь необходимо трансформировать ось ОСТ в квадрат синуса угла падения для целевой границы. Приведенная аппроксимация допустима для малых углов наклона и малых диапазонов изменения параметра. (Для AVO-анализа истинный коэффициент отражения Rрр аппроксимируется прямой, определяемой интерсептом А и градиентом В. Это геометрическая основа AVO-метода.)
Для уверенного определения углового коэффициента отражения, данные до суммирования должны подвергаться специальной обработке (динамические коррекции за геометрическое расхождение, поверхностно-согласованное масштабирование амплитуд, фазово-частотные коррекции сигнала, поверхностно-согласованная деконволюция, подавление кратных волн, преобразование NMO, DMO, миграция до суммирования).
AVO-обработка заключается в преобразовании удалений ПП-ПВ в Sin2 и для каждой сейсмограммы ОСТ в целевых интервалах, расчет интерсептов А и градиентов В с формированием кубов этих параметров.
При интерпретации используют классификацию поведения AVO-параметров для случая газонасыщенного песчаника перекрытого глинами. Выделяют 4 класса в зависимости от соотношения относительных импедансов насыщенного пласта и вмещающих пород.
| кл | Относительный импеданс | квадрант | А | В | Изменение амплитуды от удаления |
| I | Выше, чем в покрывающих породах | Q4 | + | - | уменьшение |
| II | Относительно такой же, как в покрывающих г. п. | Q2, Q3, Q4 | + или - | + или - | увеличение или уменьшение, может измениться знак |
| III | Ниже, чем в покрывающих г. п. | Q3 | - | - | увеличение |
| IV | Ниже, чем в покрывающих г. п. | Q2 | - | + | увеличение |
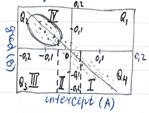
В зависимости в какой квадрант попадают точки определяется характер насыщения.
AVA-анализ – анализ зависимости амплитуды отражения от азимута (для выделения коллекторов):
1. удобно в анизотропной среде,
2. можно выйти на ориентацию трещиноватости.
Важно при разработке месторождений, чтобы был максимальный поток флюида и дебиты
2. Телеграфные уравнения переменного электромагнитного поля, их трансформации для зон волнового и квазистационарного приближений.
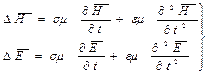
Уравнения, которым удовлетворяют векторы Н и Е в любой точке заданной среды (σ, ε, μ), называют телеграфными уравнениями.
а) в случае, если 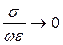 (высокие частоты, плохо проводящая среда) телеграфные уравнения преобразуются в волновые
(высокие частоты, плохо проводящая среда) телеграфные уравнения преобразуются в волновые
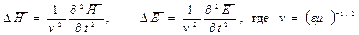 - скорость распространения электромагнитных волн.
- скорость распространения электромагнитных волн.
Пренебрежение токами проводимости в условиях высокочастотного электромагнитного взаимодействия называют волновым приближением.
б) в случае, если 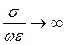 (низкие частоты, хорошо проводящая среда) телеграфные уравнения преобразуются в уравнения теплопроводности:
(низкие частоты, хорошо проводящая среда) телеграфные уравнения преобразуются в уравнения теплопроводности:
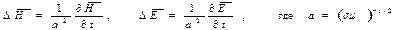 - параметр токопроводности.
- параметр токопроводности.
Пренебрежение токами смещения в условиях низкочастотного электромагнитного взаимодействия называют квазистационарным приближением.
Понятия о геологических объектах, седиментационных комплексах, формациях, цикличности осадочных образований. Понятия о сейсмогеологических объектах, сейсмоциклиты, сейсмофации, сейсмические комплексы.
Дата добавления: 2015-03-19; просмотров: 4426;
