Теоретическое введение. Термодинамические соотношения, определяющие величины теплоёмкостей при постоянном давлении ( ) и при постоянном объёме ( )
Термодинамические соотношения, определяющие величины теплоёмкостей при постоянном давлении ( 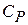 ) и при постоянном объёме (
) и при постоянном объёме ( 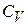 ), приведены в работе 1-20 “ Определение отношения теплоемкостей для воздуха методом адиабатического расширения”. Там же отмечено, что отношение
), приведены в работе 1-20 “ Определение отношения теплоемкостей для воздуха методом адиабатического расширения”. Там же отмечено, что отношение 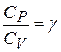 определяет скорость распространения звука в газах. Поэтому, измеряя величину скорости звука в газе, можно определить значение адиабатической постоянной
определяет скорость распространения звука в газах. Поэтому, измеряя величину скорости звука в газе, можно определить значение адиабатической постоянной 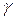 .
.
Рассмотрим, чем определяется скорость звуковых волн в газе и как она зависит от температуры. Звуковыми или акустическими волнами называют упругие волны малой интенсивности, т.е. слабые механические возмущения (деформации), распространяющиеся в упругой среде. В сплошной среде любую малую деформацию можно представить в виде элементарных деформаций растяжения (сжатия) и сдвига. Поэтому упругие свойства изотропных твердых тел вполне определяются двумя упругими константами – модулем Юнга 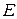 (растяжение, сжатие) и модулем сдвига
(растяжение, сжатие) и модулем сдвига 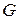 (чистый сдвиг). И, соответственно, в твердых телах могут распространяться продольные волны (волны сжатия, растяжения) и поперечные волны (волны сдвига).
(чистый сдвиг). И, соответственно, в твердых телах могут распространяться продольные волны (волны сжатия, растяжения) и поперечные волны (волны сдвига).
Что же касается газов, то они в отличие от твердых тел способны как угодно изменить свою форму под действием сколь угодно малых сил. Лишь для изменения самого объема газа, как и для твердых тел, необходимы конечные внешние силы. Т.е. газы ведут себя как упругие тела только в отношении изменения объема. Из двух элементарных деформаций – растяжения (сжатия) и сдвига – только первая связана с изменением объема. Поэтому только в отношении деформации растяжения и сжатия газы ведут себя как упругие тела. Однако и в отношении этой деформации есть существенное различие в поведении газов от твердых тел. Твердое тело можно растянуть или сжать в каком–либо одном направлении. Его можно также сжать во всех направлениях, т.е. подвергнуть всестороннему сжатию или растяжению. В газах же имеем дело только со всесторонним сжатием (только деформации сжатия). Какой бы объем ни занимала данная масса газа, газ всегда оказывается сжатым, так как в отсутствие внешних сил объем газа будет увеличиваться беспредельно. Итак, газы ведут себя как упругие тела только в отношении деформации всестороннего сжатия.
Давление в газе зависит от степени его сжатия. Так же, как и в твердых телах, связь между давлением (напряжением) и сжатием (деформацией) определяется упругими свойствами тела. Упругие свойства газа характеризуются объемной упругостью (сжимаемостью), то есть соотношением между изменением объема (плотности) данной массы газа и изменениями давления в нем. Объемная упругость жидкостей и газов количественно может быть охарактеризована отношением действующего давления к величине относительного изменения объема, которое этим давлением вызвано.
Пусть объём газа при некотором давлении равен 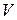 и при изменении давления на
и при изменении давления на 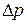 он изменится на
он изменится на 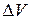 . Следовательно, относительное изменение объёма есть
. Следовательно, относительное изменение объёма есть 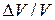 , а коэффициент сжимаемости
, а коэффициент сжимаемости 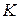 определяют как:
определяют как:
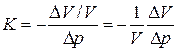 (21.1)
(21.1)
Обратная величина называется модулем сжатия:
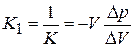 (21.2)
(21.2)
Знак минус взят затем, чтобы 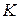 было положительно (
было положительно ( 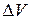 и
и 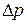 всегда противоположны по знаку).
всегда противоположны по знаку).
Если выразить (21.2) через плотность 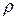 (
( 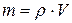 ), то получим:
), то получим:
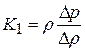 (21.3)
(21.3)
Найдем теперь, как связана скорость звуковых волн в газе с его упругими свойствами – с модулем сжатия. Звуковая волна в газе представляет собой последовательные чередующиеся области сжатия и разрежения, распространяющиеся со скоростью, зависящей от упругих свойств газа.
Как может возникнуть область сжатия в газе?
Представим себе пластину очень больших размеров, помещённую в газ (АА на рис.21.1), которой в некоторый момент времени сообщают быстрое перемещение со скоростью 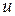 вдоль нормали к ней. В прилегающем слое газа возникнет сжатие и вследствие этого повышение давления. Это давление вызовет движение следующего слоя газа и т.д., то есть возмущение будет передаваться от слоя к слою. Возмущение за время
вдоль нормали к ней. В прилегающем слое газа возникнет сжатие и вследствие этого повышение давления. Это давление вызовет движение следующего слоя газа и т.д., то есть возмущение будет передаваться от слоя к слою. Возмущение за время 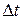 распространится до
распространится до  линии ВВ на расстояние
линии ВВ на расстояние 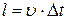 , где
, где 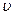 – скорость распространения упругой волны, и охватит область среды объёмом
– скорость распространения упругой волны, и охватит область среды объёмом 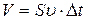 (
( 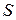 – площадь пластины) с массой
– площадь пластины) с массой 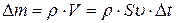 .
.
В возмущённой области всё вещество в любой момент времени движется с постоянной скоростью 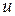 . Следовательно, изменение импульса возмущённой области равно
. Следовательно, изменение импульса возмущённой области равно 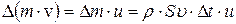 . По второму закону Ньютона изменение импульса за время
. По второму закону Ньютона изменение импульса за время 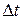 равно импульсу действующей силы:
равно импульсу действующей силы: 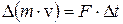 . Таким образом, сила, действующая на площадку слева, равна
. Таким образом, сила, действующая на площадку слева, равна 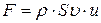 , а увеличение давления, вызванное этой силой,
, а увеличение давления, вызванное этой силой,
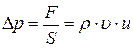 . (21.4)
. (21.4)
Распространение возмущения в газе связано с увеличением его плотности в возмущённой области на 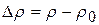 (
( 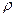 – плотность газа в области сжатия,
– плотность газа в области сжатия, 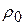 – плотность недеформированного газа). Относительное изменение плотности в возмущённой области объёмом
– плотность недеформированного газа). Относительное изменение плотности в возмущённой области объёмом 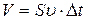 равно относительному изменению объёма при смещении пластины на
равно относительному изменению объёма при смещении пластины на 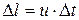 :
:
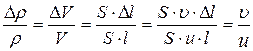 . (21.5)
. (21.5)
Из (21.4) и (21.5) получим 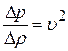 , или
, или
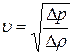 . (21.6)
. (21.6)
Таким образом, скорость распространения области сжатия в газе определяется тем, как изменяется его плотность при изменении давления.
Чтобы получить теперь окончательное выражение для скорости звука в газе, необходимо принять во внимание, что упругие свойства газов зависят от температуры. При быстром сжатии газа выделяется теплота, которая не успевает распространиться в соседние объёмы. Сжатие газа без отвода теплоты – это адиабатический процесс. При адиабатическом изменении состояния газа вместо закона Бойля-Мариотта, который справедлив при неизменной температуре (изотермическое сжатие), связь между объёмом и давлением дается уравнением Пуассона
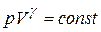 ,
, 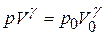 , (21.7)
, (21.7)
где 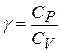 .
.
Так как плотности обратно пропорциональны объемам, то уравнение Пуассона можно переписать так: 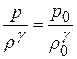 , или
, или
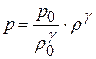 . (21.8 )
. (21.8 )
Дифференцируя (21.8), находим
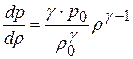 . (21.9)
. (21.9)
Если сравнить выражение 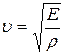 (
( 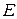 – модуль Юнга), определяющее скорость распространения продольных звуковых волн в твердых телах, и (21.6)
– модуль Юнга), определяющее скорость распространения продольных звуковых волн в твердых телах, и (21.6)
с (21.9) то видно, что величина 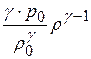 играет в газе такую же роль, какую величина
играет в газе такую же роль, какую величина 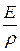 в твердом теле. Эта величина и определяет скорость распространения области сжатия. В отличие от модуля Юнга твердого тела, модуль сжатия газа зависит от того значения плотности
в твердом теле. Эта величина и определяет скорость распространения области сжатия. В отличие от модуля Юнга твердого тела, модуль сжатия газа зависит от того значения плотности 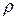 , которое имеет газ в области сжатия.
, которое имеет газ в области сжатия.
Только в том случае, когда сжатие столь мало, что можно положить 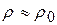 , модуль сжатия перестает зависеть от
, модуль сжатия перестает зависеть от 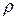 и скорость распространения области сжатия не зависит от величины сжатия (деформации).
и скорость распространения области сжатия не зависит от величины сжатия (деформации).
В этом случае, как следует из (21.9)
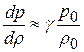 , (21.10)
, (21.10)
и скорость распространения слабых импульсов сжатия:
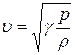 (21.11)
(21.11)
Звуковые волны можно рассматривать как ряд таких импульсов сжатия, следующих вплотную друг за другом и распространяющихся с одинаковой скоростью. Пока сжатия в звуковой волне не велики, она должна распространяться со скоростью, определяемой (21.11).
Используем уравнение состояния для идеального газа 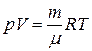 (
( 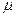 – молярная масса,
– молярная масса,  – универсальная газовая постоянная,
– универсальная газовая постоянная, 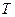 – температура) в виде
– температура) в виде 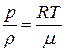 . Тогда выражение для скорости звуковых волн в идеальном газе принимает такой вид:
. Тогда выражение для скорости звуковых волн в идеальном газе принимает такой вид:
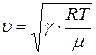 (21.12)
(21.12)
Отсюда отношение газовых теплоемкостей:
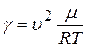 (21.13)
(21.13)
Из него следует, что для определения адиабатической постоянной 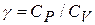 достаточно при постоянной температуре в газе измерить скорость звука.
достаточно при постоянной температуре в газе измерить скорость звука.
Отметим еще, что формула (21.12) имеет ясный физический смысл: передача возмущений в звуковой волне в газе осуществляется за счет теплового движения молекул, поэтому не удивительно, что скорость звука равна по порядку величины скорости теплового движения молекул 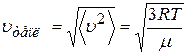 .
.
Дата добавления: 2015-03-19; просмотров: 678;
