Теоретическое введение. Гироскопом называется массивное тело, быстро вращающееся вокруг своей оси симметрии
Гироскопом называется массивное тело, быстро вращающееся вокруг своей оси симметрии. При вращении вокруг этой оси момент импульса гироскопа совпадает по направлению с осью вращения. Такое вращение устойчиво, и ось вращения гироскопа сохраняет неизменным свое направление при любом повороте или передвижении прибора.
Гироскоп – слово греческого происхождения (гирос – вращение; скопейн – видеть, наблюдать). Это название прибору дал французский физик Леон Фуко.
В общем случае под гироскопом понимают твердое тело любой формы, которое совершает вращательное движение. Земной шар, делающий один оборот за сутки, подчиняется гироскопическим законам точно так же, как технические гироскопы, вращающиеся с большей угловой скоростью относительно главной оси по сравнению со скоростями вокруг любых других осей. Гироскопами заполнен микромир: орбитальное движение и спины электронов, спин атомных ядер являются неисчерпаемой кладовой гироскопии в недрах микромира.
Гироскопические приборы и устройства находят широкое применение в различных отраслях техники. Элементарное представление об особенностях поведения гироскопа дает обыкновенный волчок с его поразительно малой восприимчивостью к воздействию внешних сил и моментов. Гироскопы чаще всего применяются для ориентации, для определения тех или иных направлений. Также гироскопы используются в горном деле для определения кривизны буровых скважин, для записи неправильностей железнодорожного пути. В авиации гироскопические приборы применяются в качестве основных чувствительных элементов (определение направления вертикали и курса), а также для измерения угловой скорости самолета.
Гироскоп в кардановом подвесе имеет три степени свободы. Если центр масс гироскопа совпадает с точкой О – точкой опоры гироскопа, то гироскоп называется уравновешенным.
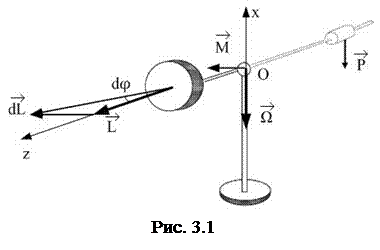 В простейшем варианте гироскоп выполняется в виде массивного диска, насаженного на вал (рис. 3.1). Для изменения направления оси гироскопа относительно неподвижной системы координат необходимо, чтобы на него действовал момент внешних сил. В таком случае наблюдается явление, называемое гироскопическим эффектом: под действием сил, которые, казалось бы, должны были вызвать поворот оси гироскопа в той плоскости, в которой лежат эти силы, в действительности ось гироскопа поворачивается вокруг оси, перпендикулярной к указанной плоскости. Такое вращение называют прецессией.
В простейшем варианте гироскоп выполняется в виде массивного диска, насаженного на вал (рис. 3.1). Для изменения направления оси гироскопа относительно неподвижной системы координат необходимо, чтобы на него действовал момент внешних сил. В таком случае наблюдается явление, называемое гироскопическим эффектом: под действием сил, которые, казалось бы, должны были вызвать поворот оси гироскопа в той плоскости, в которой лежат эти силы, в действительности ось гироскопа поворачивается вокруг оси, перпендикулярной к указанной плоскости. Такое вращение называют прецессией.
Гироскопический эффект основан на законах вращательного движения твердых тел. Пусть имеется уравновешенный гироскоп (рис. 3.1), который может вращаться вокруг осей OZ и OX. Приведем его во вращение вокруг собственной оси OZ. Тогда его момент импульса
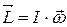 , (3.1)
, (3.1)
где I – момент инерции гироскопа относительно его оси; 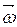 – угловая скорость собственного вращения гироскопа.
– угловая скорость собственного вращения гироскопа.
При отсутствии внешнего вращающегося момента
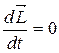 ,
, 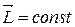 , (3.2)
, (3.2)
вектор 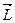 сохраняет свою величину и направление.
сохраняет свою величину и направление.
Подвесим на конец осевого стержня груз 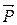 . Он будет действовать на стержень, жестко связанный с осью гироскопа. Возникнет момент этой силы
. Он будет действовать на стержень, жестко связанный с осью гироскопа. Возникнет момент этой силы 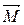 , лежащий в горизонтальной плоскости. Изменение момента импульса гироскопа под действием этого момента силы равно
, лежащий в горизонтальной плоскости. Изменение момента импульса гироскопа под действием этого момента силы равно
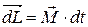 . (3.3)
. (3.3)
За время 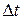 момент импульса гироскопа получит приращение
момент импульса гироскопа получит приращение
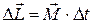 , (3.4)
, (3.4)
которое имеет такое же направление, как и 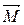 , то есть вектор
, то есть вектор 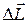 перпендикулярен вектору
перпендикулярен вектору 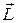 (рис.3.1). Так как момент внешних сил мал, вектор
(рис.3.1). Так как момент внешних сил мал, вектор 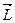 постоянен по модулю и изменяется лишь по направлению. Сила
постоянен по модулю и изменяется лишь по направлению. Сила 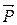 , не изменяя величины вектора
, не изменяя величины вектора 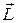 , заставляет его конец описывать окружность в горизонтальной плоскости. Таким образом, гироскопический эффект непосредственно следует из основного уравнения вращательного движения.
, заставляет его конец описывать окружность в горизонтальной плоскости. Таким образом, гироскопический эффект непосредственно следует из основного уравнения вращательного движения.
Найдём 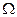 – угловую скорость прецессии, то есть дополнительного вращения оси гироскопа под действием постоянного момента сил
– угловую скорость прецессии, то есть дополнительного вращения оси гироскопа под действием постоянного момента сил 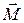 .
.
За время 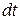 вектор
вектор 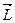 в горизонтальной плоскости повернется на угол
в горизонтальной плоскости повернется на угол 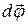 , причем, как следует из (3.3) и рис. 3.1,
, причем, как следует из (3.3) и рис. 3.1,
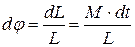 . (3.5)
. (3.5)
Таким образом, угловая скорость Ω вращения вектора 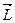 (угловая скорость прецессии) равна
(угловая скорость прецессии) равна
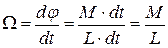 . (3.6)
. (3.6)
Поскольку 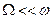 , можно считать, что и для неуравновешенного гироскопа
, можно считать, что и для неуравновешенного гироскопа 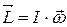 , тогда
, тогда
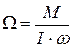 . (3.7)
. (3.7)
Дата добавления: 2015-03-19; просмотров: 1289;
