Теоретическое введение. Плотность. Распределение вещества в пространстве характеризуется некоторой величиной, называемой плотностью

Плотность. Распределение вещества в пространстве характеризуется некоторой величиной, называемой плотностью. Плотность – это масса единицы объёма вещества. Если вещество равномерно распределено в пространстве, то плотность

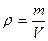(2.1)

В случае неравномерного распределения вещества плотность – это предел отношения массы 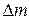к занимаемому объёму 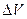при стремлении объёма к нулю:

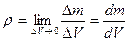(2.2)

Таким образом, для нахождения плотности необходимо знать величину массы вещества и объем, занимаемый массой. Для твердых тел величина объема зависит от их геометрической формы. Для тел правильной геометрической формы объем определяется по заранее известным формулам. Так, например, объем прямоугольного параллелепипеда определяется выражением (2.3), где a, b и h – длина, ширина и высота соответственно; сплошного цилиндра – выражением (2.3а), где 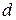– диаметр сплошного цилиндра, 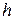– его высота; для полого цилиндра – выражением (2.3б), где 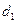, 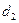– внешний и внутренний диаметры; плотности соответствующих тел можно вычислить по одной из формул (2.4).

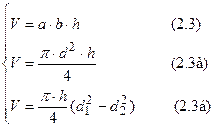
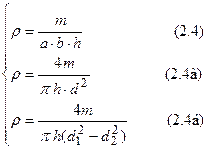
Масса твердого тела может быть определена путем взвешивания на весах. Взвешиванием называется метод определения массы тела путем сравнения его веса с весом эталонных тел – гирь. Существует большое число конструкций весов разного назначения.

Измерения.Физика является опытной наукой, поэтому умение наблюдать физические процессы и измерять разные физические величины в физике имеет особое значение.

Измерить величину – значит сравнить ее с другой однородной величиной, принятой за единицу измерения. Следовательно, под измерением следует понимать сравнение измеряемой величины с другой величиной, принятой за единицу измерения.

Такие измерения называют прямыми. При прямых измерениях определяемую величину сравнивают с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах.

Прибором обычно называют измерительное устройство, градуированное чаще всего непосредственно в единицах измерения. Измерительная установка обычно включает в себя несколько приборов и вспомогательных устройств. Резкую грань между прибором и установкой провести трудно.

Кроме измерительных приборов применяют еще и эталонные образцы, воспроизводящие ту или иную физическую величину – меры или наборы (магазины) мер. Сюда относятся гири, катушки и магазины сопротивлений и индуктивностей, нормальные гальванические элементы (эталоны электродвижущей силы) и т.д.

Измерительные приборы и установки характеризуются пределами измерения и чувствительностью.

Чувствительностью прибора или установки называют отношение перемещения указателя к вызвавшему его изменению измеряемой величины. Перемещение указателя обычно измеряют в миллиметрах или в делениях шкалы, нанесенной на приборе. На практике часто вводят вместо линейного перемещения 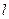угол поворота 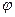. Таким образом, чувствительность 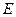определяется как

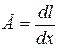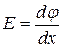или (2.5)

Иногда понятие чувствительности определяют как отношение сигналов на входе и выходе преобразователя.

В зависимости от вида функции 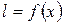чувствительность может быть либо постоянной величиной ( 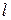пропорционально 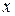), либо величиной, зависящей от 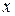. В первом случае прибор имеет линейную шкалу, во втором – нелинейную. Нелинейность шкалы обычно усложняет измерения, но иногда она позволяет увеличить чувствительность в нужной области значений измеряемой величины за счет ее уменьшения в других областях.

Наряду с чувствительностью 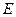при измерениях используется пороговая чувствительность, т.е. минимальное изменение измеряемой величины, которое может быть отмечено данным прибором. Этот порог, очевидно, тем ниже, чем больше .

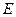Цена деления шкалы в случае приборов, шкала которых градуирована в единицах, пропорциональных линейному перемещению (т.е. в миллиметрах или в градусах), есть величина, обратная чувствительности Е

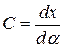(2.6)

где 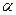по-прежнему имеет смысл линейного 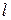или углового 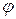перемещения. Величина 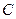удобнее, чем 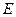, для перевода отсчетов по прибору 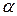в показания прибора (соответствующие значения измеряемой величины).

Точность прибора определяется погрешностью измерения этим прибором. В этом смысле между точностью и чувствительностью существует определенное соотношение. Однако такого принципа градуировки придерживаются далеко не всегда, и поэтому не следует путать точность и чувствительность. Точность прибора, как правило, указывается в его паспорте или на его шкале. Указывается максимальная абсолютная или относительная погрешность градуировки.

Приборы и меры в зависимости от точности разделяются на классы: первый (высший), второй и т.д. Допускаемые погрешности для каждого класса определяются государственными стандартами на приборы соответствующего типа. Для некоторых типов приборов и мер (например, для электроизмерительных) класс точности выражается числом, указывающим в определенной форме основную погрешность градуировки, т.е. максимальную ошибку, допускаемую при работе в нормальных условиях. Так, например, для эталонов сопротивления, индуктивности и ёмкости класс – это число, выражающее в процентах относительную погрешность воспроизведения соответствующей величины.

Если условия отклоняются от нормальных, то возникает дополнительная погрешность, величина которой определяется особыми условиями, различными для разных типов приборов.

С учетом вышеизложенного, при однократном измерении величина, измеренная прибором, не может быть точнее минимального значения цены деления шкалы данного прибора. Поскольку обычно показания прибора не совпадают с целым числом делений его шкалы, то в качестве значения измеряемой величины берется показание прибора или с недостатком или с избытком в зависимости от положения указателя. Пусть, например, при измерении миллиметровой линейкой длины край предмета оказывается между 25 и 26 делениями. Длина предмета в этом случае будет равна 25 мм с недостатком или 26 мм с избытком. На практике обычно выбирается то показание линейки, которое ближе к краю предмета. Максимальная ошибка измерения длины предмета при этом не превышает 0,5 мм, т.е. половины цены деления линейки.