Порядок выполнения работы. Задание 1. Определение погрешности прямых измерений.

Задание 1. Определение погрешности прямых измерений.

1. Бригада выполняет 50 измерений указанного преподавателем интервала времени 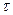. Результаты занесите в таблицу 1.1 (столбец 2).

2. По формуле 1.7 вычислите среднее арифметическое .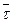

3. Найдите отклонения каждого измерения от среднего 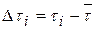(столбец 3) и 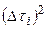(столбец 4).

4. По формуле 1.10 вычислите выборочное среднее квадратическое отклонение .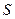

5. По таблице в приложении найти коэффициент Стьюдента t_p,N (для , ).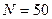

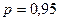6. Найдите доверительный интервал .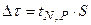

7. Запишите результат измерений промежутка времени в виде: .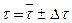

8. Определите относительную погрешность .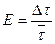

Таблица 1.1. Результаты измерений

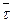
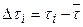
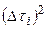
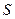
№ п/п	t					tp,N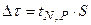
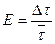
с	с	с	с2	с	-	с	-
…

Задание 2. Построение кривой распределения.

1. Выберите из результатов измерений наибольшее 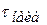и наименьшее 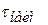значения интервалов времени. Определите промежуток изменений интервалов времени .

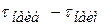2. Разбейте весь промежуток на 10 равных частей (зон)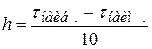

3. Заполните столбцы таблицы 1.2.

­ Подставьте конкретные числа, характеризующие границы зон (столбец 2).

­ Подсчитайте количество значений n измеренных интервалов времени t, попадающих в данную зону (столбец 3).

­ Подсчитайте относительное число измеренных интервалов времени, попадающих в каждую зону 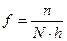(столбец 4).

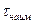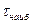4. Постройте гистограмму (см. рис.1.2). Построение выполняйте на миллиметровке! Для этого по оси абсцисс отложите значения измеренных интервалов времени, укажите на оси t наименьшее и наибольшее значения и , проведите разбиение на 10 зон шириной 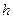. На каждой зоне постройте прямоугольник, высота которого равна относительному числу измеренных интервалов времени 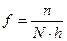. Другими словами, гистограмма отражает связь между соответствующими значениями 4 и 2 столбцов таблицы 1.3.

Таблица 1.2. Данные для построения гистограммы

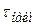
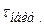
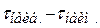
			h		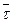S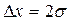
	Границы зоны	n	f
…
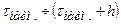
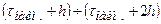
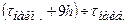
Контроль	Итого	Sn=50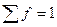

5. Нарисуйте кривую плотности распределения результатов измерений. Для этого отметьте точками середины вершин построенных прямоугольников и постройте по этим точкам плавную кривую (см. рис. 1.2).

6. Найдите среднее арифметическое .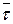

7. Найдите среднеквадратическое отклонение .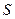

8. Найдите по графику доверительный интервал для надежности 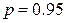. Он примерно равен .

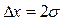Контрольные вопросы

1. Что понимается в физике под измерением? Приведите примеры.

2. Как подразделяются измерения? Поясните, приведите примеры.

3. Почему при проведении измерений появляются погрешности? Можно ли выполнить измерения "точно"?

4. Какие бывают погрешности? Дайте им характеристики, приведите примеры их появления.

5. Как учесть систематические погрешности? Промахи?

6. Какие предположения лежат в основе теории случайных погрешностей?

7. Какими основными величинами оперирует теория случайных погрешностей? Поясните их физическую суть.

8. Сколько нужно выполнить измерений, чтобы можно было воспользоваться законом нормального распределения?

9. Что такое "доверительный интервал", "надежность"?

10. Как на практике находят доверительный интервал при заданной надежности? Что такое коэффициент Стьюдента?

11. Как по виду функции Гаусса (по графику) определить дисперсию?

12. Что такое "гистограмма"?

13. Подтверждается ли в Вашей работе предположение о том, что результаты измерений подчиняются закону нормального распределения?

14. Как найти погрешность косвенных измерений?

15. Является ли полученная кривая распределения кривой Гаусса?

Используемая литература

[8]; [9].