Теоретическое введение. Простейшее движение твердого тела – плоское движение

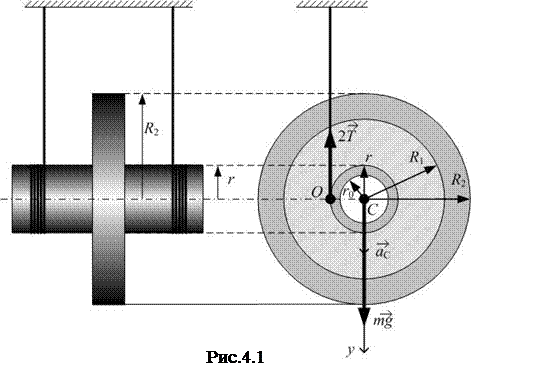Простейшее движение твердого тела – плоское движение. В этом случае каждая точка тела движется, оставаясь в одной из параллельных друг другу плоскостей. Примером плоского движения является качение цилиндра по плоскости. Другим примером является маятник Максвелла, который представляет собой диск, подвешенный на двух нерастяжимых нитях, намотанных на горизонтальную ось радиуса r (рис 4.1). Под действием силы тяжести диск опускается, и нити разматываются до полной длины. В нижнем положении раскрутившийся маховичок продолжает вращение в том же направлении и наматывает нить на ось. Дойдя до верхней точки, диск останавливается и снова начинает свое движение, совершая таким образом колебания по вертикальной прямой линии; поэтому такое устройство и называется маятником.

На примере маятника Максвелла удобно проиллюстрировать применение теоремы о движении центра масс. Так, если m – масса маятника, а T – сила натяжения каждой из двух нитей (обе они намотаны на ось маятника радиуса r), то в соответствии с теоремой о движении центра масс будем иметь:

. (4.1)

Здесь a_С– ускорение центра масс маятника в проекции на ось Y лабораторной системы координат (ее мы считаем инерциальной), g – ускорение свободного падения.

Для маятника Максвелла нетривиальным оказывается вопрос об уравнении вращательного движения (4.2):

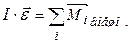, (4.2)

где 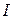– момент инерции тела, 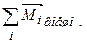– сумма моментов всех внешних сил, 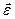– угловое ускорение тела. Если выбрать в качестве “оси моментов” ось маятника С (она движется с ускорением центра масс маятника 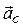), то уравнение (4.2) не будет содержать момента сил инерции, поскольку равнодействующая этих сил 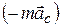, как и равнодействующая сил тяжести 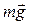, приложена в центре масс маятника, а значит, ее момент равен нулю (рис.4.1). Тогда из (4.2) имеем:

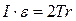, (4.3)

где радиус оси r является плечом силы натяжения относительно центра масс С; – момент инерции тела также относительно оси, проходящей через центр масс С.

Далее, два ускорения маятника Максвелла, линейное 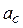и угловое ε, связаны уравнением

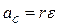. (4.4)

Таким образом, имеем систему уравнений:

Из (4.3) и (4.1):

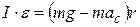и далее с учётом (4.4):

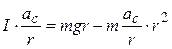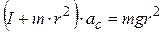, . (4.5)

Найдём ускорение центра масс, а затем угловое ускорение:

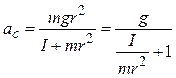, (4.6)

. (4.7)

Из (4.3) и (4.7) найдём силу натяжения нитей: ;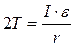

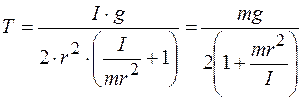. (4.8)

Из формул (4.6), (4.8) следует, что ускорение и сила натяжения нити не зависят от того, в каком направлении движется маятник - вверх или вниз. Следовательно, вес движущегося маятника 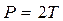не зависит от направления движения маховичка и оказывается меньше веса маятника в состоянии покоя. Из уравнения (4.6) находим момент инерции маятника:

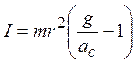. (4.9)

Ускорение 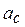находится по измеренному времени движения и пройденному пути:

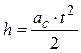, или . (4.10)

Итак, момент инерции маятника:

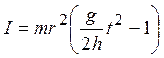. (4.11)

Поскольку силы трения не принимаются во внимание, то формулу (4.11) можно получить также из закона сохранения механической энергии. Для двух крайних положений диска:

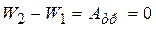или , (4.12)

откуда .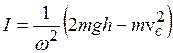

Запишем связь между линейной и угловой скоростью 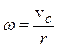, тогда

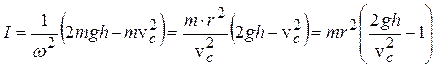. (4.13)

Из формулы пути при равнопеременном движении без начальной скорости 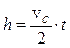можно выразить 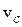и после подстановки в (4.13) получить (4.11).

<8 9 101112 13 14 >

Дата добавления: 2015-03-19; просмотров: 711;