Термодинамические процессы
Как уже отмечалось выше, система находится в состоянии равновесия если во всех точках ее объема параметры состояния р, υ, и Т имеют одинаковые значения.
Если по каким-то причинам изменяется хотя бы один параметр состояния системы, то происходит термодинамический процесс.
Например, когда в цилиндре дизельного двигателя сжимается воздух – возрастают его давление и температура и уменьшается его удельный объем. В этом случае говорят: с воздухом происходит термодинамический процесс или в воздухе происходит термодинамический процесс.
Все термодинамические процессы можно разделить на два класса: равновесные и неравновесные.
Равновесный процесс характеризуется тем, что все части системы во время такого процесса в каждый момент времени имеют одинаковые значения параметров состояния. То есть система в ходе такого процесса в каждый момент времени находится в состоянии равновесия, хотя изменение ее параметров состояния происходит. Каждый параметр изменяется так медленно, что во всем объеме системы это происходит одновременно.
Примечание:
1) На практике к равновесным процессам приближаются относительно медленные процессы.
2) В литературе равновесные процессы иногда называются квазиравновесными или обратимыми (подробнее об этом см. Приложение 4).
Все остальные процессы, для которых условия, сформулированные выше, не выполняется, называется неравновесными (необратимыми).
Таким образом, внутри системы параметры состояния (р, υ, и Т) могут изменяться двумя способами:
• параметр одинаково изменяется во всем объеме;
• в различных областях объема параметр меняется по-разному.
Процессы первого типа называются равновесными, второго – неравновесными.
В качестве примера термодинамического процесса рассмотрим процесс расширения идеального газа в теплоизолированном канале 1 с подвижными поршнями 2, рис. 3.1. Однородной термодинамической системой в этом примере является газ, заключенный между двумя подвижными поршнями. Начальное равновесное состояния системы (и здесь и далее) характеризуется цифрой 1, конечное – 2.
Соответственно начальное равновесное состояние газа характеризуется значениями параметров состояния р1, υ1 и Т1, конечное равновесное состояние – р2, υ2 и Т2.
Расширение газа от υ1 до υ2 может осуществляться двумя принципиально отличающимися способами. При очень медленном движении поршней процесс будет приближаться к равновесному расширению. При очень быстром – к сугубо неравновесному расширению в пустоту до определенного удельного объема.
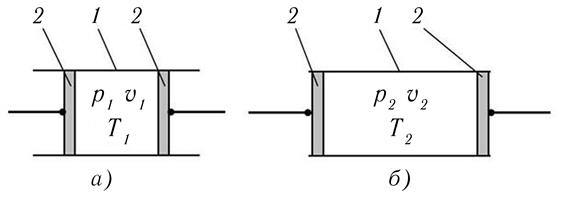Рис. 3.1. Пример термодинамического процесса 1 – 2 в газе
В первом случае температура газа понизится Т2 < Т1. Во втором останется неизменной Т2 = Т1.
Пояснить такое поведение температуры можно исходя из модели идеального газа, в котором он представляется состоящим из молекул – упругих сфер. В первом случае молекулы газа сталкиваются с удаляющимися от них поверхностями – поршнями. В результате упругого удара о такую движущуюся поверхность скорость молекул будет уменьшаться. Соответственно будут уменьшаться суммарная кинетическая энергия газа и его температура. Во втором случае молекулы всегда сталкиваются только с неподвижными поверхностями. Соответственно их скорость после таких упругих столкновений не изменяется, а значит, не изменяются суммарная кинетическая энергия газа и его температура. Дело в том, что молекулы не могут «догнать» быстрые поршни во время их перемещения на новые позиции. Таким образом, столкновений молекул с движущимися поверхностями не происходит.
В итоге можно констатировать, что идеальный равновесный процесс протекает при бесконечно медленном изменении параметров состояния. Только в этом случае во всей системе параметры будут изменяться строго одинаково.
Расчетные формулы в классической термодинамике выводятся именно для таких процессов. Однако, этими формулами можно пользоваться для реальных процессов, в которых параметры изменяются с конечными скоростями, например, при сжатии воздуха в дизельном двигателе. Как показывают оценки, в большинстве случаев ошибкой, которая появляется из-за этой конечности скоростей, можно пренебречь.
Для анализа равновесные термодинамические процессы удобно представлять в графическом виде, например, в виде графика в рυ-координатах (на рυ-плоскости). В прямоугольных координатах по оси абсцисс откладывается значение удельного объема системы, (например, газа) υ, м3/кг, по оси ординат – абсолютное давление внутри системы р, Па.
В рассматриваемом выше примере (рис. 3.1) начальная точка равновесного состояния 1, определяется путём отложения по осям параметров р1 и υ1, конечная – р2 и υ2, рис. 3.2. В ходе равновесного процесса расширения любое промежуточное состояние системы, по определению, будет также равновесным. То есть любое промежуточное состояние системы, при некоторых р и υ, также может быть отображено на рυ – плоскости точкой. Если на рυ – плоскости, изобразить все точки промежуточных состояний системы, то они сольются и образуют собой непрерывную линию, которая называется линией процесса или уравнением процесса. С точки зрения математики эта линия иллюстрирует функциональную зависимость абсолютного давления внутри системы р от значения её удельного объема р = р(υ).
Из этого следует, что идеальный равновесный процесс можно изобразить на рυ – плоскости в виде непрерывной линии. (В дальнейшем будет показано, что это справедливо и для других координатных осей).
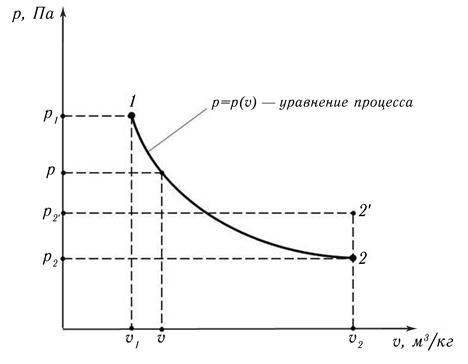
Рис. 3.2. Графическое представление процессов расширения газа в установке, изображенной на рис. 3.1
Касательно неравновесного процесса расширения в пустоту до определенного удельного объема υ2 следует отметить, что всё время процесса система (газ между поршнями) находится в неравновесном состоянии, так как параметры состояния в различных точках объёма имеют разные значения. С течением времени, давление и температура по всему объёму выравняются и система придёт в конечное состояние равновесия – точка 2′ с параметрами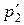 
и υ2. При этом, как уже отмечалось, температура, а значит и давление, в точке 2′ больше, чем в точке 2, что и отражено на рис. 3.2.
Таким образом понятно, что неравновесный процесс на рυ – плоскостив виде линии отображен быть не может. На этой плоскости можно отобразить только его начальное равновесное состояние (точка 1) и конечное равновесное состояние (точка 2′), которое наступит по прошествии некоторого времени после окончания процесса. Это время, за которое система приходит в состояние равновесия, называется временем релаксации.
Дата добавления: 2015-03-19; просмотров: 1721;