Уравнение состояния идеального газа. Идеальная газовая смесь

Уравнение состояния термодинамической системы определяется экспериментально. Оно показывает, каким образом в любом равновесном состоянии системы ее параметры р, υ, Т связаны между собой.

Идеальным газом в термодинамике считается газ, у которого параметры состояния связаны между собой соотношением:

p υ = R T, (2.1)

где р, υ, и Т – абсолютное давление, Па, удельный объем, м³/кг, и абсолютная температура, К, газа; R – газовая постоянная – экспериментально определенная константа, имеющая свое постоянное значение у каждого газа, Дж/(кг ∙ К).

Выражение (2.1) называется уравнением Клапейрона. Из (2.1) путем преобразований можно получить уравнение Клапейрона-Менделеева, привлекая для этого данные из следствия закона Авогадро (подробнее см. Приложение 2):

p υ = 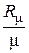T, (2.2)

где R_μ – универсальная газовая постоянная, R_μ = 8,314 Дж/(моль·К); μ – молярная масса газа (всегда известная величина, т.к. всегда известно для какого газа ведется расчет), кг/моль.

Уравнение (2.1) или (2.2) называется уравнением состояния идеального газа, так как, зная любые два параметра состояния, из них всегда можно определить третий.

Экспериментально установлено, что для большинства газов и газовых смесей в достаточно широком диапазоне давлений и температур уравнения (2.1) и (2.2) можно считать справедливыми.

Идеальной газовой смесью называется смесь, состоящая из идеальных газов. Для такой смеси все термодинамические расчеты выполняются аналогично расчетам для идеальных газов. (Расчет характеристик газовых смесей приводится в Приложении 3).

Примечание:

1) Из уравнения (2.1) и (2.2) следует, что из трех параметров состояний р, υ, и Т независимыми являются только два, но любые.

Это свойство параметров состояния, как показывают эксперименты, характерно также для простых термодинамических систем, находящихся как в твёрдом, так и в жидком состояниях. То есть для однозначного определения состояния и характеристик термодинамической системы достаточно знать любые два из трех ее параметров состояния.

2) Формулы (2.1) и (2.2) позволяют проводить расчёты для чистых идеальных газов. Однако если расчёты проводятся для смеси, состоящей из идеальных газов, то этими зависимостями также можно пользоваться, записав их в виде:

p_см υ_см = R_см T_см (2.1^*)

или

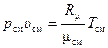, (2.2^*)

где p_см, T_см и υ_см – абсолютное давление смеси, Па, температура смеси, К, и удельный объём смеси (величина обратная плотности смеси), м³/кг, соответственно; R_см – газовая постоянная смеси, Дж/(кг ∙ К); μ_см – кажущаяся молярная масса смеси, кг/моль.

Значения, входящих в (2.1^*) и (2.2^*) величин υ_см, R_см, μ_см, определяются по всегда заданному в расчётах химическому составу газовой смеси (подробнее см. Приложение 3).

3) Уравнение состояния идеального газа достаточно хорошо описывает поведение реальных газов при высоких температурах и относительно низких давлениях. Однако, когда температура и давление таковы, что газ близок к конденсации, то формула (2.1) приводит к весьма неточным результатам. Для таких случаев необходимо пользоваться другими уравнениями состояния реальных газов.

Одним из первых примеров уравнения состояния реальных газов является уравнение, предложенное в 1873 году голландским физиком Ван-дер-Ваальсом:

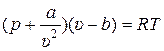, (2.3)

где a и b – по мысли Ван-дер-Ваальса размерные константы, имеющие своё значение для каждого вещества, не зависящие от температуры, плотности и давления.

Как видно из (2.3) это уравнение отличается от уравнения Клапейрона (2.1) двумя поправками: объёмной поправкой b и поправкой на так называемое внутреннее давление .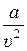

Для разряженных газов (когда поправка 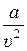мала в сравнении с «р» и когда «b» мало в сравнении с «υ») уравнение (2.3) совпадает с уравнением идеального газа (2.1). Для сжатых газов уравнение (2.3) обычно оказывается неточным. Исследование показали, что в действительности «a» и «b» являются функциями температуры и объёма.

Главная ценность уравнения (2.3) в том, что качественно оно не теряет смысла при переходе к жидкому состоянию.

Для реальных газов имеются и другие уравнения состояния. В общем виде их можно представить функциональной зависимостью вида:

F(p, υ, T) = 0.(2.4)

где F – некоторая непрерывная функция трёх переменных p, υ и T.

Общую зависимость (2.4) можно представить в более удобном для дальнейшего анализа реальных газов виде:

p = f (υ, T), (2.5)

где f – некоторая непрерывная функция двух переменных υ и T, получить вид которой для конкретного газа и определённых условий можно экспериментальным путём.

Выражение (2.5) можно рассматривать как общую форму записи уравнения состояния некоторого реального (не идеального) газа.