Центр тяжести твердого тела

Центром тяжести твердого тела называется неизменно связанная с этим телом точка С, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.

Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.

Существуют два способа определения центра тяжести тела: аналитический и экспериментальный. Аналитический способ определения центра тяжести непосредственно вытекает из понятия центра параллельных сил.

Координаты центра тяжести, как центра параллельных сил, определяются формулами:

; ; ,

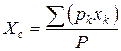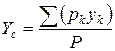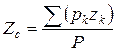где Р - вес всего тела; 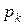- вес частиц тела; 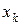, , 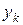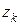- координаты частиц тела.

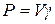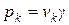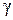Для однородного тела вес всего тела и любой её части пропорционален объёму: , , где - вес единицы объёма, V - объем тела. Подставляя выражения P, 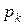в формулы определения координат центра тяжести и, сокращая на общий множитель 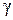, получим:

; ; .

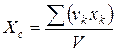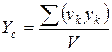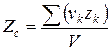Точка С, координаты которой определяются полученными формулами, называется центром тяжести объема.

Если тело представляет собой тонкую однородную пластину, то центр тяжести определяется формулами:

; ,

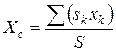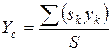где S – площадь всей пластины; 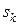- площадь её части; 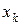, , 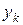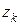- координаты центра тяжести частей пластины.

Точка С в данном случае носит название центра тяжести площади.

Числители выражений, определяющих координаты центра тяжести плоских фигур, называются статическими моментами площади относительно осей у и х:

; .

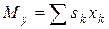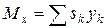Тогда центр тяжести площади можно определить по формулам:

; .

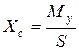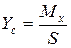Для тел, длина которых во много раз превышает размеры поперечного сечения, определяют центр тяжести линии. Координаты центра тяжести линии определяют формулами:

; ; ,

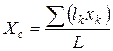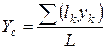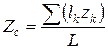где 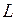- длина всей линии; 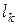- длина ее частей; 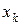, , 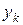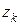- координата центра тяжести частей линии.