Центр параллельных сил
Рассмотрим две параллельные, направленные в одну сторону силы  1, и
1, и  2, , приложенные к телу в точках А1 и А2 (рис. 6.1). Эта система сил имеет равнодействующую
2, , приложенные к телу в точках А1 и А2 (рис. 6.1). Эта система сил имеет равнодействующую 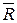 =
=  1+
1+  2, линия действия которой проходит через некоторую точку С, лежащую на прямой A1A2. Положение точки С можно найти с помощью теоремы Вариньона:
2, линия действия которой проходит через некоторую точку С, лежащую на прямой A1A2. Положение точки С можно найти с помощью теоремы Вариньона: 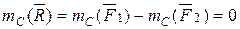 .
.
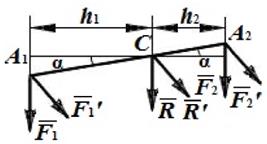
Рис. 6.1
Если повернуть силы  1 и
1 и  2 около точек А1 и А2 в одну сторону и на один и тот же угол, то получим новую систему параллельных сал, имеющих те же модули. При этом их равнодействующая
2 около точек А1 и А2 в одну сторону и на один и тот же угол, то получим новую систему параллельных сал, имеющих те же модули. При этом их равнодействующая 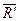 будет также проходить через точку С, и для нее будет сохраняться вышеуказанное равенство. Такая точка называется центром параллельных сил.
будет также проходить через точку С, и для нее будет сохраняться вышеуказанное равенство. Такая точка называется центром параллельных сил.
Рассмотрим систему параллельных и одинаково направленных сил  1,
1,  2,
2,  3,..
3,..  n, приложенных к твердому телу в точках А1, А2 , А3 ,… Аn (рис. 6.2). Эта система имеет равнодействующую
n, приложенных к твердому телу в точках А1, А2 , А3 ,… Аn (рис. 6.2). Эта система имеет равнодействующую 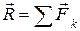 .
.
Если каждую силу системы повернуть около точек их приложения в одну и ту же сторону и на один и тот же угол, то получатся новые системы одинаково направленных параллельных сил с теми же модулями иточками приложения. Равнодействующая таких систем будет иметь тот же модуль R, но всякий раз другое направление. Сложив силы  1 и
1 и  2, найдем что их равнодействующая
2, найдем что их равнодействующая 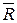 1 (на рис. 6.2 не показана) будет всегда проходить через точку с1, положение которой определяется равенством
1 (на рис. 6.2 не показана) будет всегда проходить через точку с1, положение которой определяется равенством 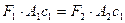 . Сложив далее
. Сложив далее 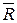 1 и
1 и  3, найдем их равнодействующую, которая всегда будет проходить через точку с2, лежащую на прямой с1А3 . Доведя процесс последовательного сложения сил до конца, придем к выводу, что равнодействующая
3, найдем их равнодействующую, которая всегда будет проходить через точку с2, лежащую на прямой с1А3 . Доведя процесс последовательного сложения сил до конца, придем к выводу, что равнодействующая 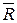 всех сил действительно всегда будет проходить через одну и ту же точку С, положение которой по отношению к точкам А1, А2, А3,… Аn будет неизменным.
всех сил действительно всегда будет проходить через одну и ту же точку С, положение которой по отношению к точкам А1, А2, А3,… Аn будет неизменным.
Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол называется центром параллельных сил (рис. 6.2).
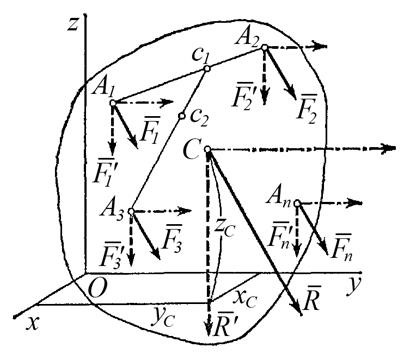
Рис.6.2
Определим координаты центра параллельных сил. Поскольку положение точки С по отношению к телу является неизменным, то ее координаты от выбора системы координат не зависят. Повернем все силы около точек их приложения так, чтобы они стали параллельны оси Оz и применим к повернутым силам теорему Вариньона. Так как 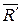 является равнодействующей этих сил, то, согласно теореме Вариньона, имеем
является равнодействующей этих сил, то, согласно теореме Вариньона, имеем 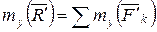 , т.к.
, т.к. 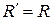 ,
, 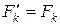 , получим
, получим
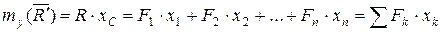 .
.
Отсюда находим координату центра параллельных сил 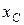 :
:  .
.
Для определения координаты 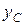 составим выражение моментов сил относительно оси Ox.
составим выражение моментов сил относительно оси Ox.
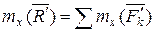 ,
, 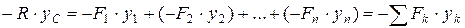 ,
,
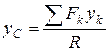 .
.
Для определения координаты 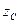 повернем все силы, чтобы они стали параллельны оси Oy, и применим к этим силам (изображенным на рисунке пунктиром с точками) теорему Вариньона, беря моменты относительно оси Ox:
повернем все силы, чтобы они стали параллельны оси Oy, и применим к этим силам (изображенным на рисунке пунктиром с точками) теорему Вариньона, беря моменты относительно оси Ox:
 ,
, 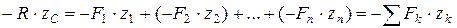 ,
,
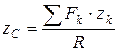 .
.
Дата добавления: 2015-03-17; просмотров: 1142;
