Прості форми кристалів кубічної сингонії

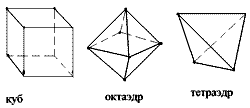
Рис. 7. Прості форми кубічної сингонії

Кристали кубічної сингонії мають свої особливі прості форми. У кристалах кубічної сингонії описані вище прості форми не можуть бути присутніми. Тут ми завжди маємо 4 взаємно перпендикулярні осі третього порядку, тому всі прості форми кубічної сингонії – закриті. Всього є 15 простих форм, які належать тільки кристалам кубічної сингонії. Ми розглянемо п'ять головних, а останні є похідними від них.

Кубічний тетраедр – проста форма, утворена чотирьма рівними рівносторонніми трикутними гранями, перпендикулярними осям третього порядку (рис.7).

Куб – проста форма, утворена шістьма рівними попарно паралельними квадратними гранями (рис.7), що створюють один із одним кути 90^о. Грані куба перпендикулярні осям четвертого порядку (L₄).

Октаедр (від грецьк. "окта" – вісім, "едр" – грань) – проста форма, утворена вісьма рівними рівносторонніми трикутними попарно паралельними гранями (рис.7), перпендикулярними осям третього порядку (L₃).

Ромбододекаедр (від грецьк. "додека" – дванадцять) – проста форма, утворена 12 рівними гранями, що мають форму ромба (рис. 8).

Пентагондодекаедр (від грецьк. "пента" - п'ять) – закрита проста форма, яка складається з 12 рівних граней, що мають форму неправильних п'ятикутників (рис. 8).

Рис. 8. Прості форми вищої Рис. 9. Кристали, утворені

категорії комбінацією двох простих форм: 1 – призми і біпіраміди, 2 – куба і октаедра