Прості форми кристалів нижчої і середньої категорій

Проста форма кристала- сукупність граней, взаємозв'язаних симетричними операціями даного класу симетрії. Всі грані, створюючи одну просту форму кристала, повинні бути рівні за розміром і формою. У кристалі можуть бути присутніми одна або декілька простих форм. Поєднання декількох простих форм називають комбінацією. Прості форми умовно поділяють на:

· закриті – прості форми, грані яких повністю замикають укладений між ними простір, як, наприклад, куб, октаедр, тетраедр, дипіраміда.

· відкриті прості форми – не замикають простір і не можуть існувати самостійно, а тільки в комбінаціях. Наприклад, призма, пінакоїд, моноедр.

Рис.5. Прості форми нижчої категорії: моноедр (1), пінакоїд (2), діедр (3)

У нижчих сингоніях можливі такі відкриті прості форми (рис. 5):

Моноедр (від грецьк. "моно" – один, "едра" – грань) – проста форма, представлена однією єдиною гранню. Моноедромом є, наприклад, піраміда.

Пінакоїд (від грецьк."пінакс" – дошка) – проста форма, що складається з двох рівних паралельних граней, часто орієнтованих назад.

Діедр (від грецьк."ді" – два, "едр" – грань) – проста форма, утворена двома рівними пересічними гранями, що створюють "прямий дах".

Ромбічна призма – проста форма, яка складається з чотирьох рівних, попарно паралельних граней, які в перетині утворюють ромб.

Ромбічна піраміда – проста форма складається з чотирьох рівних пересічних граней; у перетині також утворює ромб.

Існують наступні закриті прості форми нижчих сингоній:

Ромбічна дипіраміда - дві ромбічні піраміди, складені основами. Форма має вісім рівних граней, що становлять у поперечному перетині ромб.

Ромбічний тетраедр – проста форма, чотири грані якої мають форму косокутних трикутників і замикають простір.

У сингоніях середньої категорії з перелічених вище простих форм можуть бути присутніми тільки моноедр і пінакоїд.

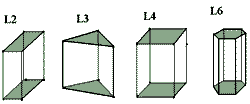
Рис. 6. Зовнішній вигляд призматичних кристалів: 1 – ромбічна призма; 2 – тригональна призма; 3 – призма тетрагона; 4 – гексагональна призма

Відкритими простими формами сингоній середньої категорії будуть призми і піраміди (рис.6).

Тригональна призма (від грецьк."гон" – кут) – три рівні грані, пересічних за паралельними ребрами і створюючих у перетині рівносторонній трикутник.

Призма (від грецьк."тетра" – чотири) тетрагона – чотири рівні попарно паралельні грані, що створюють у перетині квадрат.

Гексагональна призма (від грецьк."гекса" – шість) – шість рівних граней, пересічних за паралельними ребрами і створюючих у перетині правильний шестикутник.

Назви дитригональних, дитетрагональних і дигексагональних отримали призми з подвоєним числом граней, коли всі грані рівні, а однакові кути між гранями чергуються через один.

Піраміди – прості форми кристалів середньої категорії можуть бути, як і призми, тригональними (дитригональними), тетрагонами (дитетрагональними), гексагональними (дигексагональними). Вони утворюють у перетині правильні багатокутники. Грані пірамід розташовуються під косим кутом до осі симетрії вищого порядку.

У кристалах середньої категорії зустрічаються і закриті прості форми. Таких форм декілька.

Дипіраміди – прості форми, утворені двома рівними пірамідами, складеними основами. У таких формах відбувається подвоєння піраміди горизонтальною площиною симетрії, перпендикулярною головній осі симетрії вищого порядку. Дипіраміди, як і прості піраміди, залежно від порядку осі можуть мати різні форми перетину. Вони можуть бути тригональними, дитригональними, тетрагонами, дитетрагональними, гексагональними і дигексагональними.

Ромбоедр – проста форма, яка складається з шести граней у вигляді ромбів і нагадує витягнутий або сплюснутий по діагоналі куб. Він можливий тільки в тригональній сингонії. Верхня і нижня група граней повернені відносно один одного на кут 60^о таким чином, що нижні грані розташовуються симетрично між верхніми.

У сингоніях середньої категорії вірогідні також скаленоедри, тетраедр тетрагона і трапецоедри.