Идентификация моделей и интервалы восстановления
Теоретическое обоснование системы ОТС. За счет чего могут приносить эффект автоматизированные системы контроля функционирования оборудования и средства технической диагностики? Повышение информированности обслуживающего персонала, безусловно, расширяет маневренность производства, но это сложно связать с экономией затрат. На наш взгляд, в первую очередь эффект связан с автоматизацией. Меньше становится трудозатрат по ревизии оборудования, когда разборка – сборка узлов производится с целью выявления возможных дефектов. Система диагностики становится эффективной, когда средства диагностики сочетаются с диагностическими моделями, для которых строятся деградационные модели по выбранным диагностическим признакам и показателям. Эти модели должны создаваться механиками, обслуживающими оборудование для конкретных условий его эксплуатации. Разработчикам

средств диагностики решение таких вопросов не свойственно.
Сущность преимущества ОТС заключается в более полном использовании ресурсов элементами конструкций. Чтобы обосновать это, рассмотрим деградационную модель старения во времени эксплуатации t линейного типа (1, рис. 8.2, а):
 (8.2)
(8.2)
где Dt и D0 – соответственно, текущее и начальное значение диагностического параметра,
v – скорость (интенсивность) деградационного процесса.
Последний параметр функции (8.2) – нормально распределенная случайная величина, медианное значение которой vм и её среднеквадратическое отклонение (СКО) Svm обычно устанавливаются косвенно по времени до выхода из строя элемента механической системы по допускаемому значению [D]:
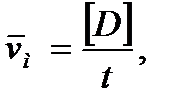
 (8.3)
(8.3)
где SD – СКО величины [D].
Учитывая нормальность распределения параметра D, гарантированное время наработки на отказ для допускаемой вероятности безотказной работы (ВБР) будет:
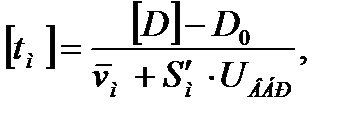 (8.4)
(8.4)
где UР = UВБР – нормированный квантиль нормального распределения, соответствующий [ВБР].
| arctg VM |
| 6 • S VM |
| UP |
| O |
| UВБР |
| t max |
| t |
| D0 |
| t |
| [ t ]M |
| [D] |
| D |
а
| arctg VФ |
| 6 • S VФ |
| UP |
| O |
| UВБР |
| t max |
| t |
| D0 |
| ti |
| [t]Ф |
| [D] |
| D |
| arctg VФ |
| [t]'Ф |
| S‘D |
| Δti |
| ti-1 |
| t |
| Di-1 |
| Di |
б
Рис. 8.2 Прогнозирование функций распределения сроков службы 2 по моделям старения 1 при системе обслуживания «по нормативу» (ППР,а) и системе обслуживания по техническому состоянию (ОТС,б).
Величина [t]м определяется по функции распределения наработки на отказ (2, рис. 8.2). Такая схема обслуживания «по нормативу», основанная на статистических данных о наработке на отказ, принята в системе ППР. При ОТС оценка скорости деградационного процесса 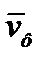 рассчитывается по результатам измерений величины Di через интервалы времени Δti в i-ый раз контроля [7]:
рассчитывается по результатам измерений величины Di через интервалы времени Δti в i-ый раз контроля [7]:
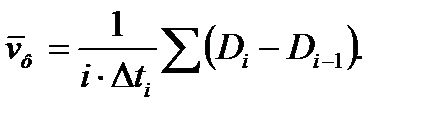 (8.5)
(8.5)
СКО величины VФ в этом случае определяется так [4]:
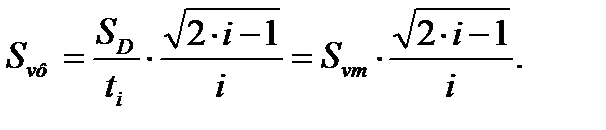 (8.6)
(8.6)
Величина фактического СКО скорости Svф значительно ниже своего модельного (априорного) значения Svm, поскольку второй сомножитель (иногда называемый коэффициентом перемешивания реализаций) меньше единицы. Вдобавок, здесь значение SD определяется погрешностью измерительных устройств, которая на порядок меньше разброса измеряемого параметра. Поэтому после подстановки в (8.4) вместо модельных параметров фактических значений гарантированная наработка на отказ [t]ф, увеличивается относительно исходного [t]м. На практике это дает рост межремонтных периодов и сроков службы. Поскольку поведение технологических машин нельзя прогнозировать со 100% - ой уверенностью, то приближение к этой вероятности путем выявления в случайных факторах детерминированной составляющей заставляет полнее раскрываться потенциалу конструкции. При мониторинге происходит идентификация деградационной модели, в которую первоначально входят статистические характеристики Vм и Svм, отражающие свойства генеральной совокупности идентичных систем, а затем эти характеристики замещаются оценками VФ и Svф. Именно такова каноническая точка зрения на принцип ОТС [7].
Из изложенного вытекают два следствия.
1. Для технологического оборудования важно знать не только его состояние на момент контроля, но и иметь надежный прогноз на период работы, исключающий ремонтные воздействия. После контроля в момент времени ti прогнозирование осуществляется по средней оценке VФ. Но не обязательно дальнейший процесс будет происходить с той же скоростью. Чем короче время экстраполяции процесса (шаг), тем надежнее прогноз работоспособности. Увеличить шаг, можно используя более достоверные и сложные модели, нуждающиеся в длительном экспериментальном обосновании. Поэтому процесс мониторинга заключается в пошаговом переназначении сроков службы - от проектного ресурса к исходному и далее - к остаточному ресурсу (рис.8.1) [8].
2. Увеличить точность прогноза остаточного ресурса можно путем увеличения числа измерений i. При периодическом контроле практически сузить разброс величины наработки на отказ можно в 2-3 раза, переходя от нескольких контролей к нескольким десяткам. При сплошном контроле модель становится детерминированной и рассеяние долговечности будет определяться точностью измерения диагностического параметра D. Соответствующая этому величина S´D существенно меньше оценки SD, что дает дополнительное увеличение межремонтного периода [t]´ф> [t]ф (рис. 8.2, б). Таким образом, предпочтительнее сплошной контроль диагностических параметров с пошаговой оценкой остаточного ресурса.
В качестве функции отклика D в деградационных моделях кинетического типа могут использоваться различные диагностические параметры, но наиболее успешно осуществляется мониторинг для коррозионных и износных явлений, когда величина D непосредственно измеряется (прямой метод). Кроме слабых прогностических возможностей, что присуще многим современным средствам диагностики (например, увеличение виброскорости в 2-3 раза до предельной происходит за короткий период катастрофического роста трещины, а до этого тренд сигнала не прослеживается), прямые методы в подавляющем большинстве указывают на неисправности машины. Они не дают информации об остаточном ресурсе конструкций, поскольку используемые диагностические параметры весьма отдаленно связаны с природой разрушения материалов. Персоналу сложно определить приближение конструкции к предельному состоянию, чтобы принять компенсирующие мероприятия. В этом отношении интересны физические способы контроля, тесно связанные с усталостным повреждением материалов (например, магнитный и акустикоэмиссионный способы контроля кожухов доменных печей и воздухонагревателей [9]), но о широком их применении в ГМК говорить еще рано.
Для иллюстрации принципиального различия двух подходов к техническому обслуживанию «по нормативу» и «по состоянию» рассмотрим распространенную ситуацию.
Пусть динамика определяющего параметра задается в виде
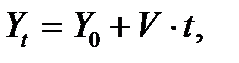 (8.7)
(8.7)
где Y0 – известная величина;
V – нормально распределенная случайная величина с математическим
определением 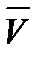 и дисперсией Sv2, то есть
и дисперсией Sv2, то есть 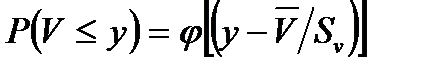 , а
, а
распределение φ(х) задано выражением
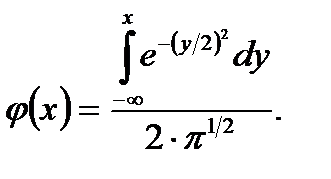 (8.8)
(8.8)
Таким образом, параметр Yt распределен нормально с математическим ожиданием 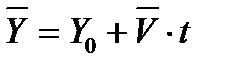 и дисперсией
и дисперсией 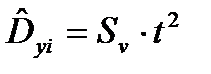 .
.
Рассмотрим одностороннюю допустимую область и монотонно возрастающие реализации стохастического процесса {Yt}t≥0 для P(V≥0)=1. Вероятность безотказной работы:
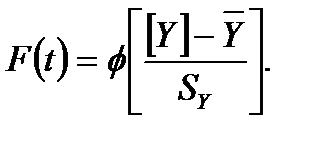 (8.9)
(8.9)
Интервал восстановления τв рассчитывается из условия 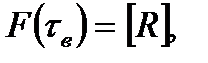 где [R] – заданное значение вероятности безотказной работы.
где [R] – заданное значение вероятности безотказной работы.
Из (8.9) следует равенство:
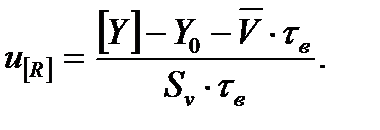 (8.10)
(8.10)
Отсюда находим
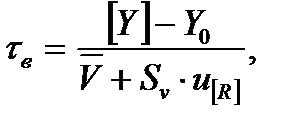 (8.11)
(8.11)
где u[R] – квантиль стандартного нормального распределения.
Для примера рассмотрим кривошипно-шатунный механизм, управляющий положением рабочего органа. В его шарнирных соединениях происходит износ, ведущий к зазорам и образованию мертвого хода Y, который является диагностическим параметром с линейной моделью изменения. При этом среднее значение зазоров 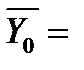 3мм, его коэффициент вариации v0=0,1, допустимое значение [Y]=13мм. Через 50 часов эксплуатации (t50) среднее значение зазора составило Y50= 5мм, а его СКО SY50=1мм. Тогда средняя скорость износа и ее СКО будут:
3мм, его коэффициент вариации v0=0,1, допустимое значение [Y]=13мм. Через 50 часов эксплуатации (t50) среднее значение зазора составило Y50= 5мм, а его СКО SY50=1мм. Тогда средняя скорость износа и ее СКО будут: 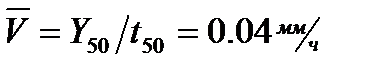 ,
, 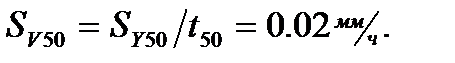
Эти данные годятся для оценки исходного ресурса, если закон распределения параметров модели (в данном случае нормальный) исследован. На стадии проектирования следует также учитывать вариацию начального параметра. Это ведет к росту СКО скорости (интенсивности) изнашивания: 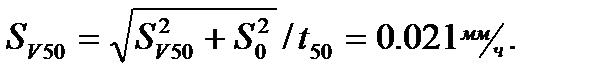
В табл. 8.1 приведены значения интервалов восстановления, обеспечивающих различные значения вероятностей безотказной работы.
При обслуживании по фактическому состоянию в модели (8.7) скорость рассчитывается по результатам измерений Yt.
Будем считать, что систематическая погрешность измерений отсутствует, а случайная нормально распределенная погрешность характеризуется дисперсией S02. в качестве неизвестной величины V принимаем ее оценку, полученную, например, методом наименьших квадратов:
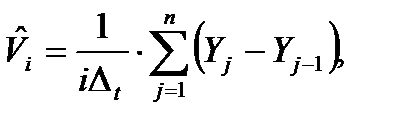 (8.12)
(8.12)
где Yj – измерение параметра Yt в дискретный момент времени jΔt;
i – число измерений.
Оценка 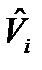 имеет нормальное распределение с математическим ожиданием
имеет нормальное распределение с математическим ожиданием 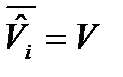 и дисперсией
и дисперсией 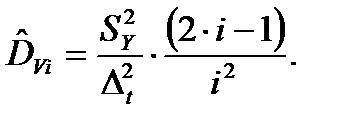
Интервалы восстановления τв исполнительного механизма в часах Таблица 8.1
| № | Этап оценки ресурса и характер определения параметра | Глубина идентификации модели | Sv, мм/ч | [R] | 0,9 | 0,95 | 0,99 | 0,999 |
| u[R] | 1,282 | 1,645 | 2,324 | 3,092 | ||||
| k | 3,066 | 4,513 | 10,104 | 140,7 | ||||
| Назначенный ресурс, априорные значения параметра | Принятое распределение V и Y0 | 0,021 | ||||||
| Исходный ресурс, выборочный контроль параметра | Известное распределение Yi | 0,020 | ||||||
| Исходный ресурс, выборочный контроль параметра | Стохастический характер изменения Yi | 0,020 | ||||||
| Остаточный ресурс, мониторинг параметра | Фактические значения Y0 | 0,0009 |
При подстановке оценки Vi в модель (8.7) получаем нормально распределенную оценку текущего значения параметра Yt:
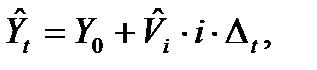 (8.13)
(8.13)
с математическим ожиданием 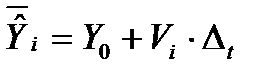 и дисперсией
и дисперсией 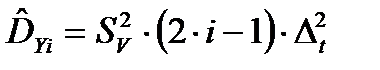 .
.
Оценка 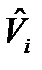 позволяет построить прогнозируемое значение определяющего параметра Yi+m (m=0, 1, 2,……):
позволяет построить прогнозируемое значение определяющего параметра Yi+m (m=0, 1, 2,……):
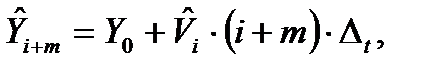 (8.14)
(8.14)
с математическим ожиданием 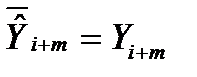 и дисперсией
и дисперсией 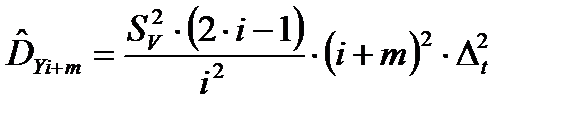 .
.
Таким образом, случайная величина
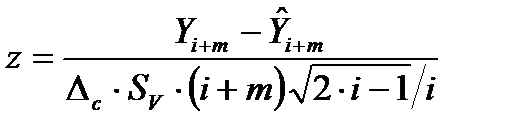 (8.15)
(8.15)
Имеет стандартное нормальное распределение и интервал восстановления (i+m)∙Δt определяется аналогично (8.10)
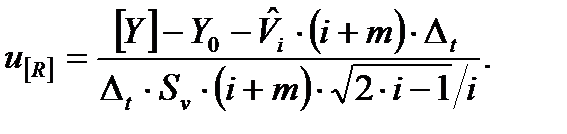 (8.16)
(8.16)
Отсюда находим
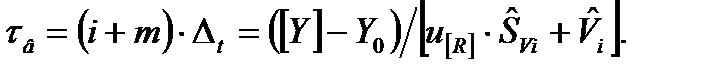 (8.17)
(8.17)
Выражения (8.10) и (8.17) аналогичны, однако в (8.17) вместо математического ожидания и среднеквадратического отклонения, характеризующих свойства генеральной совокупности идентичных систем, появляется оценка Viиее среднеквадратическое отклонение SVi, характеризующее процесс идентификации модели старения конкретной единственной системы.
Учитывая, что погрешность измерения выбирается, как правило, не менее чем в 10 раз меньше разброса измеряемого параметра в партии изделий, проведем численное сравнение двух подходов. Пусть [Y]=3 мм, Yв=13 мм, V50ч=0,04 мм/ч, Δt=5 ч, i=10, σ0=0,1 мм. Расчет дает значение SV50ч=8,72∙10-4 мм/ч.
В таблице 8.1 приведены результаты расчета интервалов восстановления для различных значений вероятностей безопасной работы. Таблица 8.1 иллюстрирует преимущества подхода к обслуживанию по фактическому состоянию.
В заключение заметим, что при достаточно большом числе измерений, используемых для неизвестной скорости V, дисперсия ее оценки стремится к нулю, модель старения становится детерминированной и с вероятностью R3≈1 может быть установлен необходимый момент восстановления. Так, в данном числовом примере при 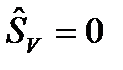 получим τв=250 ч.
получим τв=250 ч.
Рассмотренный подход может быть обобщен на любую параметрическую модель старения, при этом основное внимание уделяется методу идентификации модели.
При идентификации модели динамики параметров достаточно часто дисперсия оценки параметра точно неизвестна и оценивается по той же выборке. Действительно, модели изменения параметров в процессе эксплуатации систем являются в основном эмпирическими. Поэтому разброс оценки определяется не только случайными погрешностями измерений, но и неизвестными случайными флюктуациями параметра от модельного значения. В таком случае задача несколько усложняется, поскольку случайная величина 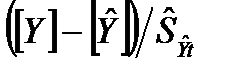 уже не будет иметь нормальное распределение вероятностей.
уже не будет иметь нормальное распределение вероятностей.
Рассмотрим более подробно распределение случайной величины 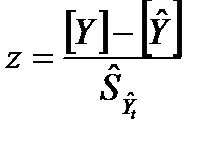 . Представим случайную величину z в виде
. Представим случайную величину z в виде
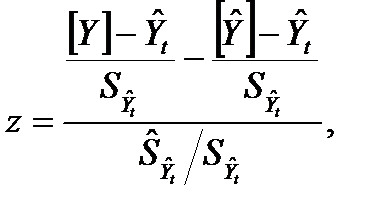 (8.18)
(8.18)
где n –объем выборки, по которой производилась оценка Yt. Первое слагаемое числителя совпадает с предыдущим случаем, то есть
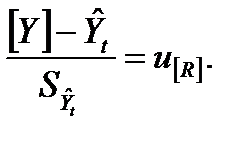 (8.19)
(8.19)
Второе слагаемое числителя – случайная величина, имеющая стандартное нормальное распределение, то есть
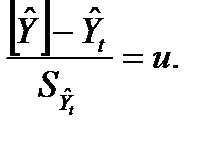 (8.20)
(8.20)
Знаменатель представляет собой случайную величину, имеющую распределение 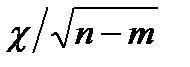 ,
,
где χ2 – распределение Пирсона с (n-m) степенями свободы;
m – число оцениваемых параметров (в данном примере m=1).
В результате случайная величина z имеет нецентральное t - распределение Стьюдента с параметром нецентральности u[R].
В такой ситуации, если принять доверительную вероятность равной [R], распределение ресурса будет характеризоваться статистикой k, являющейся математическим ожиданием нормально распределенной случайной величины 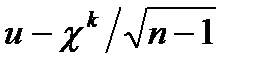 [7]:
[7]:
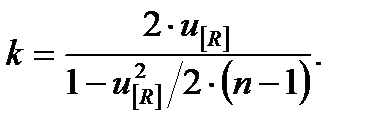 (8.21)
(8.21)
В таблице 8.1 приведены результаты расчетов значений характеристик k при различных [R] и n.
Алгоритм расчета времени восстановления в данном случае будет иметь вид
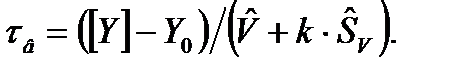 (8.22)
(8.22)
В таблице 8.1 приведены значения времени восстановления для рассматриваемого примера при замене СКО SV на ее оценку 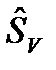 той же величины.
той же величины.
Анализ значений в таблице 8.1 показывает, что неопределенность оценки дисперсии снижает эффект от перехода к обслуживанию по техническому состоянию. Это ставит высокие требования к точности идентификации деградационных процессов старения при эксплуатации изделия.
Практические аспекты перехода к ОТС. Внимательное изучение возможностей штатных (встроенных) систем контроля работы оборудования в ГМК дает основание считать, что они приносят пользу, которая не вполне связанна с переходом на ОТС. Учитывая высокую аварийность оборудования и осуществление ремонтов, преимущественно, по факту отказов, можно судить о том, что, фактически, не действует система ППР на многих производствах. А значит, применение систем контроля рабочих параметров процессов и машин, что трактуется как переход на ОТС, сразу может не ощущаться. И без наличия системы мониторинга, ориентированной на обнаружение неисправных состояний, ресурс конструкций используется полностью, хотя и путем аварий. Лишь некоторые системы мониторинга (все в прокатном производстве) ориентированы на оценку остаточного ресурса основных узлов оборудования, что дает возможность полностью получить эффект от ОТС.
Построение реально работающей системы мониторинга технологического оборудования в инженерно-организационном отношении – трудоемкая задача. Она осложняется субъективными причинами мотивационного характера. Речь идет о том, что на ранних стадиях эксплуатации оборудования, когда оно имеет малую степень износа, необходимость обслуживания по техническому состоянию не ощущается. Надежность поддерживается планово-предупредительной системой ремонтов. Эта система становится малоэффективной на поздних стадиях эксплуатации, когда, с одной стороны, необходимо сдерживать возрастающие расходы на техническое обслуживание, связанные с преждевременной заменой не выработавших технический ресурс узлов, а с другой стороны. нужно застраховаться от аварий, что наиболее существенно сказывается на годовой производительности. Но чтобы на таких стадиях обоснованно оценивать техническое состояние, необходимо знать историю эксплуатации от ее начала.
Чтобы успешно осуществить переход к новой системе ТОиР целесообразно придерживаться ряда рекомендаций:
1. Следует создавать многоцелевую систему, обрабатывающую показания различных источников информации, в которую на уровне подсистемы входит функция оценки остаточного ресурса базовых узлов.
2. Менеджмент предприятий и обслуживающий персонал должен понимать, что никакие рекламные заявления производителей и поставщиков средств диагностики не решают проблему перехода на ОТС без диагностических алгоритмов. Поэтому необходимо сосредоточить усилия на разработке диагностических моделей и алгоритмов, доведя процедуру оценки технического состояния до технологии, доступной инженерному составу.
3. Диагностические алгоритмы должны обеспечивать точность, достоверность и пошаговую заблаговременность прогнозирования.
Чтобы отвечать этим требованиям, необходимо придерживаться принципа поэтапного назначения ресурса, а также использовать аппарат ресурсной механики для построения деградационных моделей. Переход к ОТС также должен быть поэтапным. На первом этапе необходимо наладить информационную систему по истории эксплуатации сменных узлов и сплошной контроль наработки базовых узлов. Он может осуществляться от естественных (штатных) источников информации. Второй этап связан с использованием специализированных средств диагностики. Причем для оценки остаточного ресурса основная информация идет от сплошного контроля, а периодический контроль специализированными средствами позволяет идентифицировать условия эксплуатации, отражающиеся на интенсивности процесса накопления повреждений.
Дата добавления: 2015-03-14; просмотров: 1089;
