Показатель риска для систем

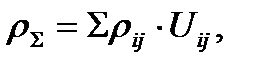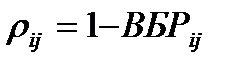Оценить состояние сложных и простых систем по показателям отдельных их элементов позволяет риск – анализ. В общем виде риск системы ρ_Σ можно определить по формуле полной вероятности где - вероятность отказа (риск) i – го элемента, имеющая смысл частоты аварий, а U_i – некий уровень значимости [12]. Если U_i выразить через натуральный ущерб, то данное выражение представляет каноническую трактовку риска, измеряемого через ущерб в единицу времени (5).

Для функции надежности экспоненциального вида в области высоких вероятностей

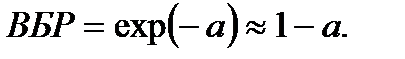
Откуда следует, что a_ij=ρ_ij, то есть накопленное повреждение вполне характеризует риск эксплуатации и потерю работоспособности. Тогда возможно определять риск системы как

.

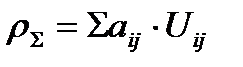Поскольку a_ij изменяется со временем наработки, то подобно изменяется и величина ρ_Σ.

Чтобы избежать вычисления ущерба в натуральных единицах, удобно использовать для U_ij относительные величины. Применяя в этом качестве отношение безусловной эффективности к эффективности идеальной машины, определяют надежность сложной технической системы [12]. Таким образом, решается противоречие, присущее правилу ΠR_ij, поскольку тогда коэффициент U_ij характеризует уже систему в целом, но вероятность отказа ρ_ij относится к отдельному элементу.

В практике обеспечения надежности известна процедура анализа последствий отказов FMEA, в которой критичность отказа элемента C_ij оценивается в баллах. Тогда значимость U_ij определяется через относительную критичность отказа:

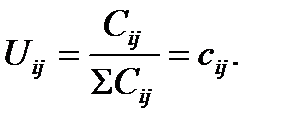
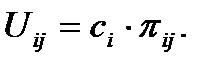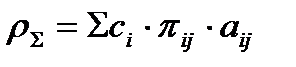Зная долю отказов соответствующей категории тяжести в возможных отказах системы π_ij, уровень значимости вычисляют как Тогда [12].

Если использовать ресурсную модель для определения ВБР, то в ней автоматически учитывается «временной» фактор эксплуатации, и необходимость контроля накопленного повреждения a_ij отпадает. Тогда для ФРД логнормального вида lgT_p и для нормального закона распределения времени наработки t_p риск системы с достаточной точностью можно определить как:

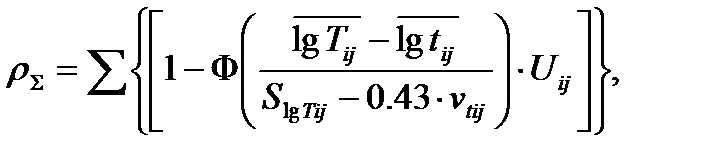(3.2)

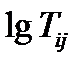где и 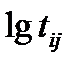- соответственно, средний логарифм ресурса и логарифм средней наработки, для элемента I и повреждающего процесса j;

S и v – соответственно, СКО ресурса и коэффициент вариации наработки.

При изложенных методах оценки риска с учетом потенциального ущерба возможны сложности с обоснованием предельной величины [ρ_Σ]. Без ее значения не возможно диагностировать работоспособные состояния. Более объективно оперировать с частотной составляющей риска ρ_i. Такой оперативной характеристикой риска выступает отношение вероятности отказа к ВБР: 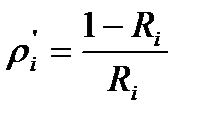[13].

Тогда предельная величина ρ^’ будет равняться единице. Это происходит когда R=0.5, что указывает на бесполезность детерминированных расчетов для оценки безопасности. При диагностировании практический интерес представляют сроки наработки, когда R→0,98….0,95 и необходимо принимать решение о дальнейшей эксплуатации элемента. В таких областях оперативная характеристика риска, фактически, совпадает с вероятностью отказа: 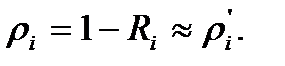Поэтому частотная составляющая рисков элементов может характеризовать безопасное состояние системы.