НА РЕГУЛЯРНОМ ВОЛНЕНИИ

Разделим все члены уравнений (3.39) на соответствующие первые коэф-фициенты

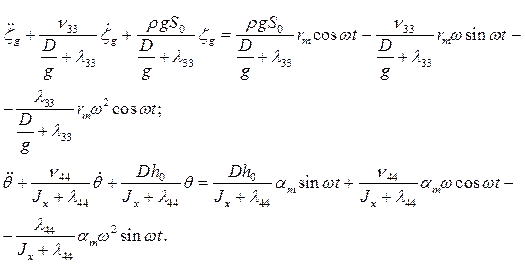(3.40)

Введя обозначения в соответствии с (3.11), (3.12) и (3.20), получим

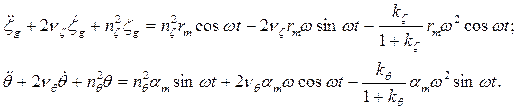(3.41)

Здесь по аналогии с формулой (3.20)

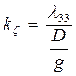. (3.42)

Решение проведем на примере уравнения бортовой качки. Это уравнение является дифференциальным, второго порядка, линейным, неоднородным. Решение такого уравнения ищется в виде суммы двух решений:

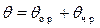, (3.43) где 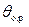- общее решение однородного уравнения, т.е. уравнения, в правой части которого стоит 0 (уравнение качки судна на тихой воде). Такое решение

имеет затухающий характер и довольно быстро исчезает. Его можно не учитывать в случае продолжительного воздействия волнения;

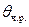- решение неоднородного уравнения в форме правой части. Тогда будет

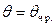
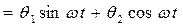. (3.44)

Таким образом, можно отметить, что на регулярном волнении корабль качается с частотой, равной частоте волнения. Такая качка называется вынужденной. На нерегулярном же волнении при набегании каждой новой волны возбуждаются новые свободные колебания, а вынужденные не успевают развиться. Такая качка называется возмущенной. При этом корабль качается с собственной частотой.

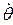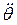Определив производные и , подставив их в исходное уравнение и при-равняв коэффициенты отдельно 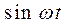при и при 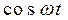слева и справа, получим решение в виде:

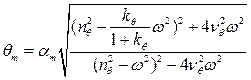; (3.45)

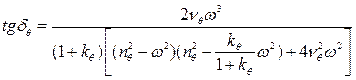, (3.46)

где 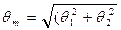- амплитуда вынужденной качки корабля на регулярном волнении; - фаза колебаний судна по отношению к колебаниям волновой поверхности.Они возникают при переходе к одночленной форме записи в решении (3.44)

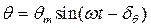.(3.44´)

После ряда преобразований выражения (3.45) и (3.46) можно переписать в безразмерной форме

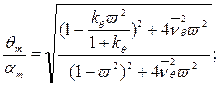(3.45´)

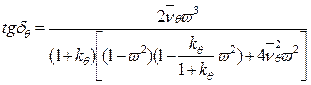, (3.46´)

где 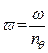- безразмерная частота волны; 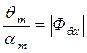- модуль передаточной функции, или коэффициент динамичности, характеризующий способность корабля, как динамической системы, реагировать на внешнее возмущение;

Для кораблей, у которых дифракционные силы малы, часто пренебрегают ими, т.е. в правых частях уравнений (3.40) остаются только первые члены. Такие уравнения называются укороченными:

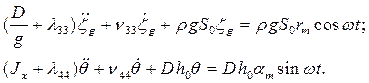(3.40´)

При этом решения (3.45´) - (3.46´) упростятся и получатся в виде:

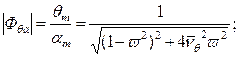(3.47)

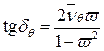. (3.48)

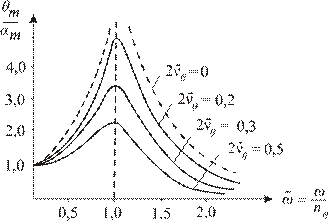
Зависимость 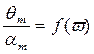называется амплитудно - частотной характе-ристикой (АЧХ). На рис. 3.10 приведена АЧХ для решения в форме (3.47), на рис. 3.11 - в форме (3.45´).

На всех графиках видны зоны резонансов пр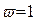и или 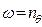, т.е. при сов-падении частоты волнения с собственной частотой судна. Отношение 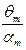при этом равно

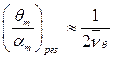, (3.49)

т.е. оно обратно пропорционально безразмерному коэффициенту затухания.

Рис.3. 10. АЧХ, полученная из решения укороченного

уравнения бортовой качки

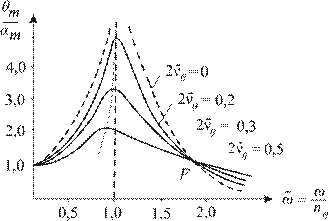
Рис. 3.11. АЧХ, полученная из решения полного

уравнения бортовой качки

Зависимость 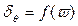называется фазово-частотной характеристикой (ФЧХ). Ее вид при решении уравнений в форме (3.48) и (3.46´) приведен на рис. 3.12, а) и б) соответственно.

Необходимо отметить, что при резонансе .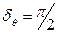

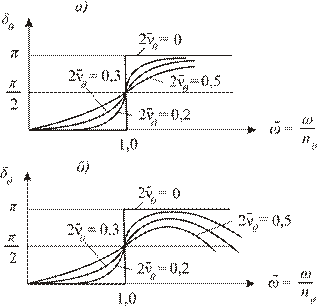
Рис. 3.12. ФЧХ, полученные из решения укороченного и полного уравнений качки

Аналогичным образом можно получить при решении полного уравнения вертикальной качки:

амплитудно - частотную характеристику

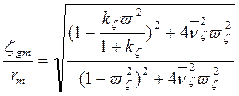(3.50)

и фазово - частотную характеристику

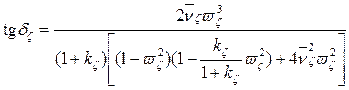, (3.51) где 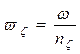; (3.52)

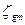- амплитуда вертикальной качки.

Соответствующие АЧХ приведены на рис. 3.13. Ввиду того, что безразмер-ный коэффициент затухания при вертикальной качке обычно имеет большую величину, безразмерные резонансные амплитуды невелики.

Укороченные уравнения вертикальной качки рассматривать нет необходи-мости, поскольку дифракционные силы для этого вида качки могут быть одного порядка с крыловскими. Пренебрежение дифракционными силами может привести к значительным погрешностям при определении амплитуд качки.

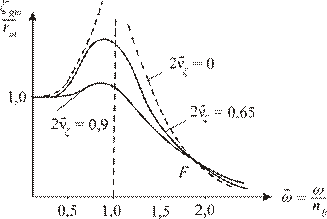
Рис. 3.13. Амплитудно-частотные характеристики

вертикальной качки